
- Geometric modeling and 3D shape analysis
- Spatial data structures and algorithms
- Topology-based machine learning
- Topology-based geospatial data visualization
- Mesh-based terrain and surface modeling
- Applications to environmental data modeling and analysis
Leila De Floriani
Professor
Department of Geographical Sciences & University of Maryland Institute for Advanced Computer Studies (UMIACS)
University of Maryland, College Park
Email: deflo(at)umd.edu
News
-
Leila De Floriani
-
Leila De Floriani nominated to the Scientific Council of the Italian Scientists and Scholars in North America Foundation (ISSNAF) | Link
-
Leila De Floriani interviewed by Renata Johnson from UMD in Spring 2024 | Link
-
An article on appeared on IEEE Spectrum in November 2023 featuring Leila De Floriani as Division VIII Director | Link
-
-
Yunting Song successfully defended her PhD dissertation titled Efficient terrain analysis of point cloud datasets on a decomposition-based data representation in May 2024. She will be joining Google after her graduation in July 2024.
-
Noel Dyer successfully defended his PhD dissertation titled Visualization, Data Quality, and Scale in Composite Bathymetric Data Generalization. May, 2024.
-
Xin Xu successfully defended his PhD dissertation titled Topology-based individual tree mapping from lidar point clouds. October, 2023.
-
Our proposal, An Open-Source Library for Processing Forest Point Clouds Based on Topological Data Analysis, has been selected for funding by NASA HPOSS program. August, 2024. | Link
-
Our paper, Critical Features Tracking on Triangulated Irregular Networks by a Scale-Space Method, authored by Haoan Feng, Yunting Song, and Leila De Floriani, has been accepted as a FULL paper and for an ORAL presentation at the ACM SIGSPATIAL Conference 2024.
-
Our paper, Efficient representation and analysis for a large tetrahedral mesh using Apache Spark, authored by Yuehui Qian, Guoxi Liu, Federico Iuricich, Leila De Floriani has been accepted by IEEE Topological Data Analysis and Visualization (TopoInVis). 2024.
-
Our paper, ImplicitTerrain: a Continuous Surface Model for Terrain Data Analysis, authored by Haoan Feng, Xin Xu, and Leila De Floriani has been accepted for presentation in CVPR 2024 Workshop, Implicit Neural Representation for Vision. June, 2024. | Link
-
Our paper, Parallel Topology-aware Mesh Simplification on Terrain Trees, authored by Yunting Song, Riccardo Fellegara, Federico Iuricich, and Leila De Floraini has been accepted by ACM Transactions on Spatial Algorithms and Systems. March, 2024. | Link
-
Our paper, Chart features, data quality, and scale in cartographic sounding selection from composite bathymetric data, authored by Noel Dyer, Christos Kastrisios, and Leila De Floriani has been accepted for publication in Geo-spatial Information Science. October, 2023. | Link
-
Yunting Song finished her summer internship at Google. August, 2023.
Previous news
Team
Principal Investigator
Graduate Students
Former Ph.D. Students & Collaborators
Selected Publications

Parallel Topology-aware Mesh Simplification on Terrain Trees
Yunting Song, Riccardo Fellegara, Federico Iuricich, and Leila De FlorianiACM Transactions on Spatial Algorithms and Systems, 10 , pages 1-39, 2024.
Abstract
We address the problem of performing a topology-aware simplification algorithm on a compact and distributed data structure for triangle meshes, the Terrain trees. Topology-aware operators have been defined to coarsen a Triangulated Irregular Network (TIN) without affecting the topology of its underlying terrain, i.e., without modifying critical features of the terrain, such as pits, saddles, peaks, and their connectivity. However, their scalability is limited for large-scale meshes. Our proposed algorithm uses a batched processing strategy to reduce both the memory and time requirements of the simplification process and thanks to the spatial decomposition on the basis of Terrain trees, it can be easily parallelized. Also, since a Terrain tree after the simplification process becomes less compact and efficient, we propose an efficient post-processing step for updating hierarchical spatial decomposition. Our experiments on real-world TINs, derived from topographic and bathymetric LiDAR data, demonstrate the scalability and efficiency of our approach. Specifically, topology-aware simplification on Terrain trees uses 40% less memory and half the time compared to the most compact and efficient connectivity-based data structure for TINs. Furthermore, the parallel simplification algorithm on the Terrain trees exhibits a 12x speedup with an OpenMP implementation. The quality of the output mesh is not significantly affected by the distributed and parallel simplification strategy of Terrain trees, and we obtain similar quality levels compared to the global baseline method.

ImplicitTerrain: a Continuous Surface Model for Terrain Data Analysis
Haoan Feng, Xin Xu, and Leila De FlorianiConference on Computer Vision and Pattern Recognition (CVPR), Workshop of Implicit Neural Representation for Vision, 2024.
Abstract
Digital terrain models (DTMs) are pivotal in remote sensing, cartography, and landscape management, requiring accurate surface representation and topological information restoration. While topology analysis traditionally relies on smooth manifolds, the absence of an easy-to-use continuous surface model for a large terrain results in a preference for discrete meshes. Structural representation based on topology provides a succinct surface description, laying the foundation for many terrain analysis applications. However, on discrete meshes, numerical issues emerge, and complex algorithms are designed to handle them. This paper brings the context of terrain data analysis back to the continuous world and introduces ImplicitTerrain, an implicit neural representation (INR) approach for modeling high-resolution terrain continuously and differentiably. Our comprehensive experiments demonstrate superior surface fitting accuracy, effective topological feature retrieval, and various topographical feature extraction that are implemented over this compact representation in parallel. To our knowledge, ImplicitTerrain pioneers a feasible continuous terrain surface modeling pipeline that provides a new research avenue for our community.

Chart features, data quality, and scale in cartographic sounding selection from composite bathymetric data
Noel Dyer, Christos Kastrisios, and Leila De FlorianiGeo-spatial Information Science, pages 1-26, 2023.
Abstract
Cartographic sounding selection is a constraint-based bathymetric generalization process for identifying navigationally relevant soundings for nautical chart display. Electronic Navigational Charts (ENCs) are the premier maritime navigation medium and are produced according to international standards and distributed around the world. Cartographic generalization for ENCs is a major bottleneck in the chart creation and update process, where high volumes of data collected from constantly changing seafloor topographies require tedious examination. Moreover, these data are provided by multiple sources from various collection platforms at different levels of quality, further complicating the generalization process. Therefore, in this work, a comprehensive sounding selection algorithm is presented that focuses on safe navigation, leveraging both the Digital Surface Model (DSM) of multi-source bathymetry and the cartographic portrayal of the ENC. A taxonomy and hierarchy of soundings found on ENCs are defined and methods to identify these soundings are employed. Furthermore, the significant impact of depth contour generalization on sounding selection distribution is explored. Incorporating additional ENC bathymetric features (rocks, wrecks, and obstructions) affecting sounding distribution, calculating metrics from current chart products, and introducing procedures to correct cartographic constraint violations ensures a shoal-bias and mariner-readable output. This results in a selection that is near navigationally ready and complementary to the specific waterways of the area, contributing to the complete automation of the ENC creation and update process for safer maritime navigation.
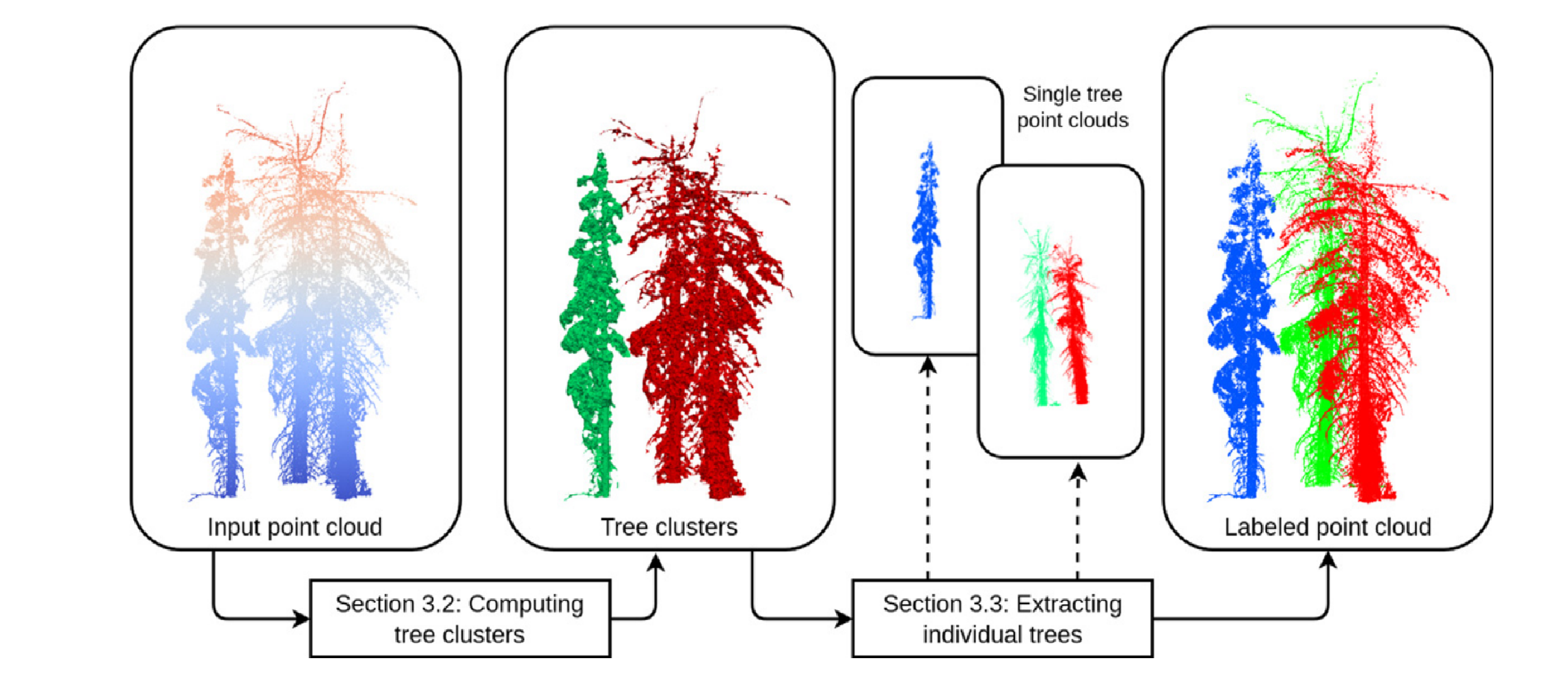
Topology-based individual tree segmentation for automated processing of terrestrial laser scanning point clouds
Xin Xu, Federico Iuricich, Kim Calders, John Armston, and Leila De FlorianiInternational Journal of Applied Earth Observation and Geoinformation, 116 , pages 103145, 2022.
Abstract
Terrestrial laser scanning (TLS) is a ground-based approach to rapidly acquire 3D point clouds via Light Detection and Ranging (LiDAR) technologies. Quantifying tree-scale structure from TLS point clouds requires segmentation, yet there is a lack of automated methods available to the forest ecology community. In this work, we consider the problem of segmenting a forest TLS point cloud into individual tree point clouds. Different approaches have been investigated to identify and segment individual trees in a forest point cloud. Typically these methods require intensive parameter tuning and time-consuming user interactions, which has inhibited the application of TLS to large area research. Our goal is to define a new automated segmentation method that lifts these limitations. Our Topology-based Tree Segmentation (TTS) algorithm uses a new topological technique rooted in discrete Morse theory to segment input point clouds into single trees. TTS algorithm identifies distinctive tree structures (i.e., tree bottoms and tops) without user interactions. Tree tops and bottoms are then used to reconstruct single trees using the notion of relevant topological features. This mathematically well-established notion helps distinguish between noise and relevant tree features.To demonstrate the generality of our approach, we present an evaluation using multiple datasets, including different forest types and point densities. We also compare our TTS approach with open-source tree segmentation methods. The experiments show that we achieve a higher segmentation accuracy when performing point-by-point validation. Without expensive user interactions, TTS algorithm is promising for greater usage of TLS point clouds in the forest ecology community, such as fire risk and behavior modeling, estimating tree-level biodiversity structural traits, and above-ground biomass monitoring.
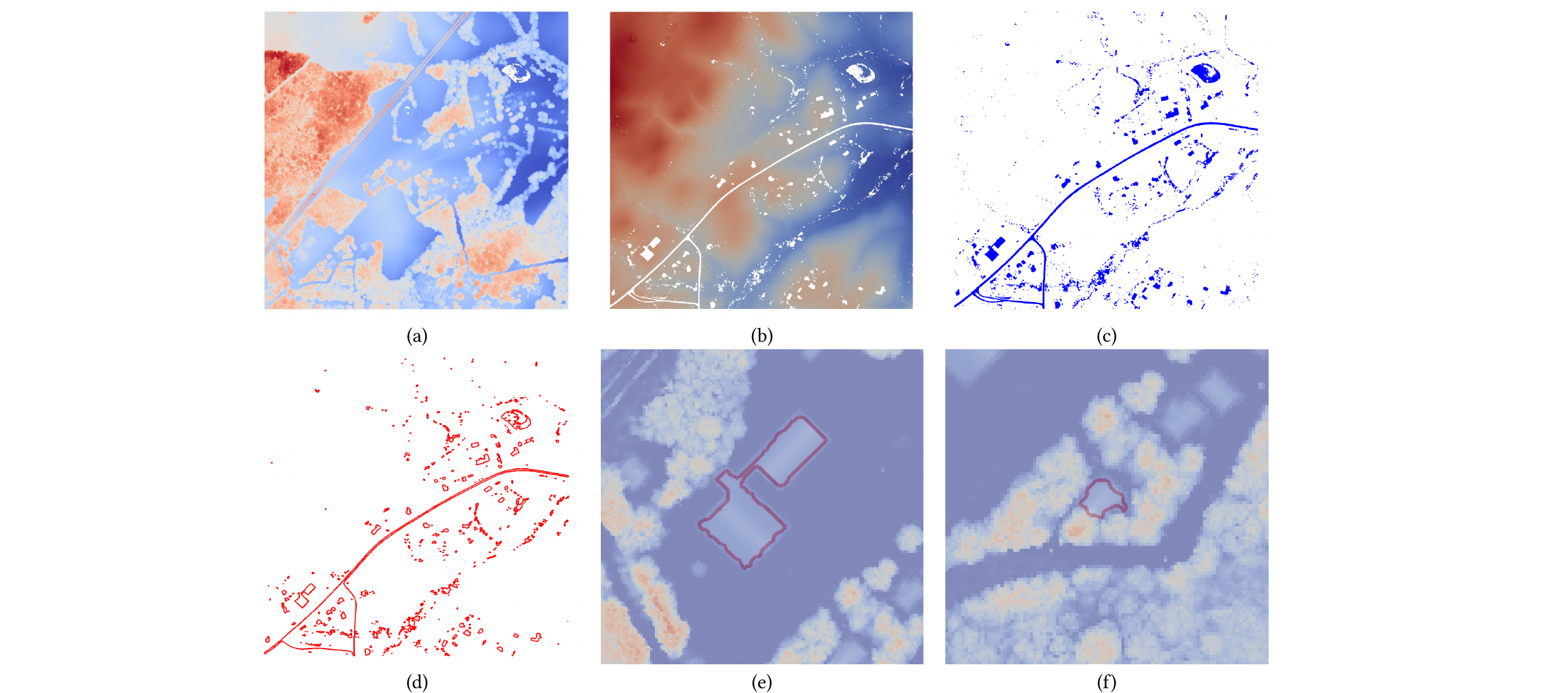
An unsupervised building footprints delineation approach for large-scale LiDAR point clouds
Xin XuProceedings of the 30th International Conference on Advances in Geographic Information Systems, pages 1-4, 2022.
Abstract
We design a novel unsupervised approach to delineate building footprints on large-scale LiDAR point clouds. By computing an α-shape on low-height points, we delineate the building bottoms on the ground. We then use the terrain ruggedness index and vector ruggedness measurement on the entire points to find flat surface areas. Finally, valid building footprints are filtered by checking flat surfaces in the detected bottom areas. Compared to the Artificial Intelligence (AI)-assisted mapping results from Microsoft Building Footprints, the accuracy of the proposed method is 17% higher in the test areas. The simple and effective pipeline makes the proposed method easy to use and suitable for a wider range of applications.

Terrain trees: a framework for representing, analyzing and visualizing triangulated terrains
Riccardo Fellegara, Federico Iuricich, Yunting Song, and Leila De FlorianiGeoInformatica (preprint), 2022.
Abstract
We propose a family of spatial data structures for the representation and processing of Triangulated Irregular Networks (TINs). We call such data structures Terrain trees. A Terrain tree combines a minimal encoding of the connectivity of the TIN with a hierarchical spatial index. Connectivity relations are extracted locally at run-time, within each leaf block of the hierarchy, based on specific application needs. Spatial queries are performed by exploring the hierarchical data structure. We present a new framework for terrain analysis based on Terrain trees. The framework, implemented in the Terrain trees library (TTL), contains algorithms for morphological features extraction, such as roughness and curvature, and for topology-based analysis of terrains. Moreover, it includes a technique for multivariate visualization, which enables the analysis of multiple scalar fields defined on the same terrain. To prove the effectiveness and scalability of such framework, we have compared the different Terrain trees against each other and also against the most compact state-of-the-art data structure for TINs. Comparisons are performed on storage and generation costs and on the efficiency in performing terrain analysis operations.
Extended version of Riccardo Fellegara, Federico Iuricich, Leila De Floriani (2017). Efficient Representation and Analysis of Triangulated Terrains. Proceedings of the 25th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems.
PDF DOI
Label-based generalization of bathymetry data for hydrographic sounding selection
Noel Dyer, Christos Kastrisios, and Leila De FlorianiCartography and Geographic Information Science, pages 1-16, 2022.
Abstract
Hydrographic sounding selection is the process of generalizing high-resolution bathymetry data to a more manageable subset capable of supporting nautical chart compilation or bathymetric modeling, and thus, is a fundamental task in nautical cartography. As technology improves and bathymetric data are collected at higher resolutions, the need for automated generalization algorithms that respect nautical cartographic constraints increases, since errors in this phase are carried over to the final product. Currently, automated algorithms for hydrographic sounding selection rely on radius- and grid-based approaches; however, their outputs contain a dense set of soundings with a significant number of cartographic constraint violations, thus increasing the burden and cost of the subsequent, mostly manual, cartographic sounding selection. This work presents a novel label-based generalization algorithm that utilizes the physical dimensions of the symbolized depth values on charts to avoid the over-plot of depth labels at scale. Additionally, validation tests based on cartographic constraints for nautical charting are implemented to compare the results of the proposed algorithm to radius and grid-based approaches. It is shown that the label-based generalization approach best adheres to the constraints of functionality (safety) and legibility.
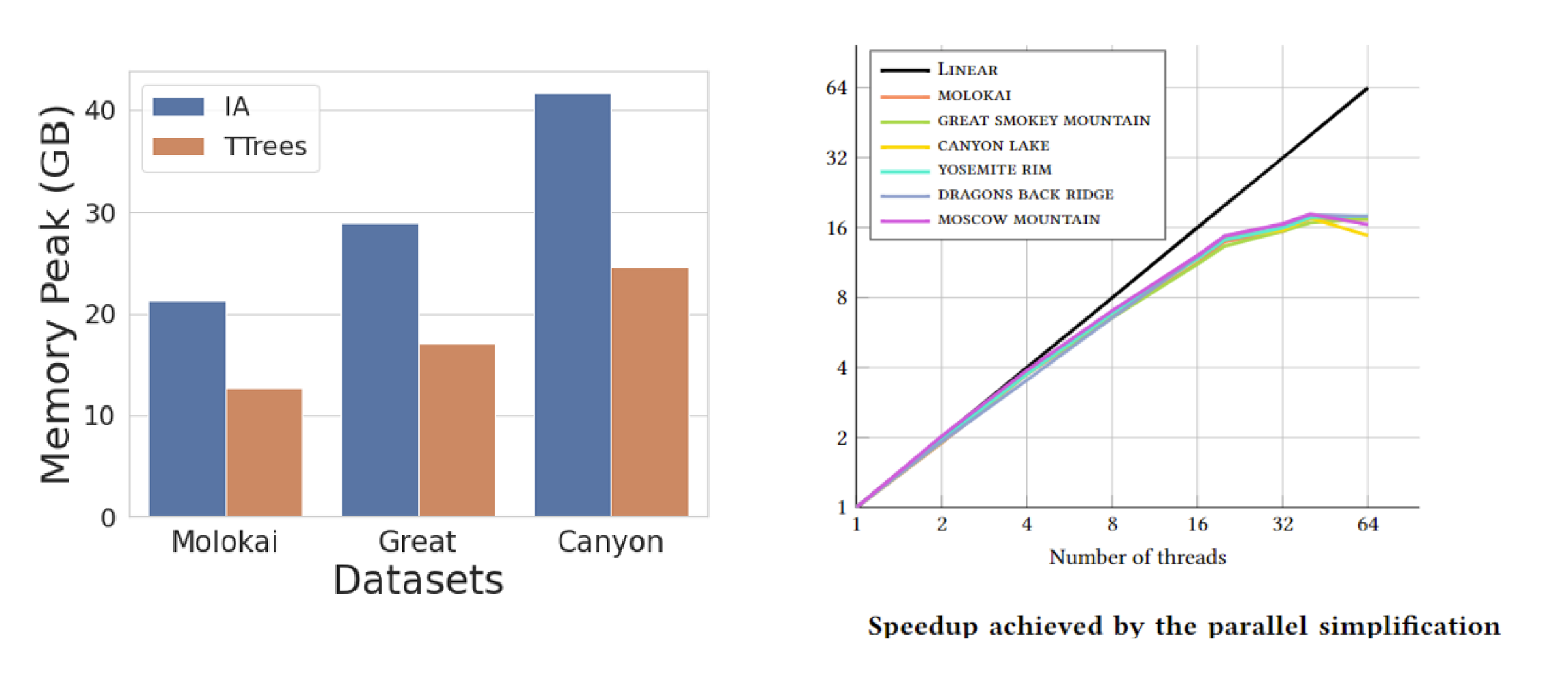
Efficient topology-aware simplification of large triangulated terrains
Yunting Song, Riccardo Fellegara, Federico Iuricich, and Leila De FlorianiProceedings of the 29th International Conference on Advances in Geographic Information Systems, pages 576–587, 2021.
Abstract
A common first step in the terrain processing pipeline of large Triangulated Irregular Networks (TINs) is simplifying the TIN to make it manageable for further processing. The major problem with TIN simplification algorithms is that they create or remove critical points in an uncontrolled way. Topology-aware operators have been defined to solve this issue by coarsening a TIN without affecting the topology of its underlying terrain, i.e., without modifying critical simplices describing pits, saddles, peaks, and their connectivity. While effective, existing algorithms are sequential in nature and are not scalable enough to perform well with large terrains on multicore systems. Here, we consider the problem of topology-aware simplification of very large meshes. We define a topology-aware simplification algorithm on a compact and distributed data structure for triangle meshes, namely the Terrain trees. Terrain trees reduce both the memory and time requirements of the simplification procedure by adopting a batched processing strategy of the mesh elements. Furthermore, we define a new parallel topology-aware simplification algorithm that takes advantage of the spatial domain decomposition at the basis of Terrain trees. Scalability and efficiency are experimentally demonstrated on real-world TINs originated from topographic and bathymetric LiDAR data. Our experiments show that topology-aware simplification on Terrain trees uses 40% less memory and half the time than the same approach implemented on the most compact and efficient connectivity-based data structure for TINs. Beyond that, our parallel algorithm on the Terrain trees reaches a 12x speedup when using 20 threads.
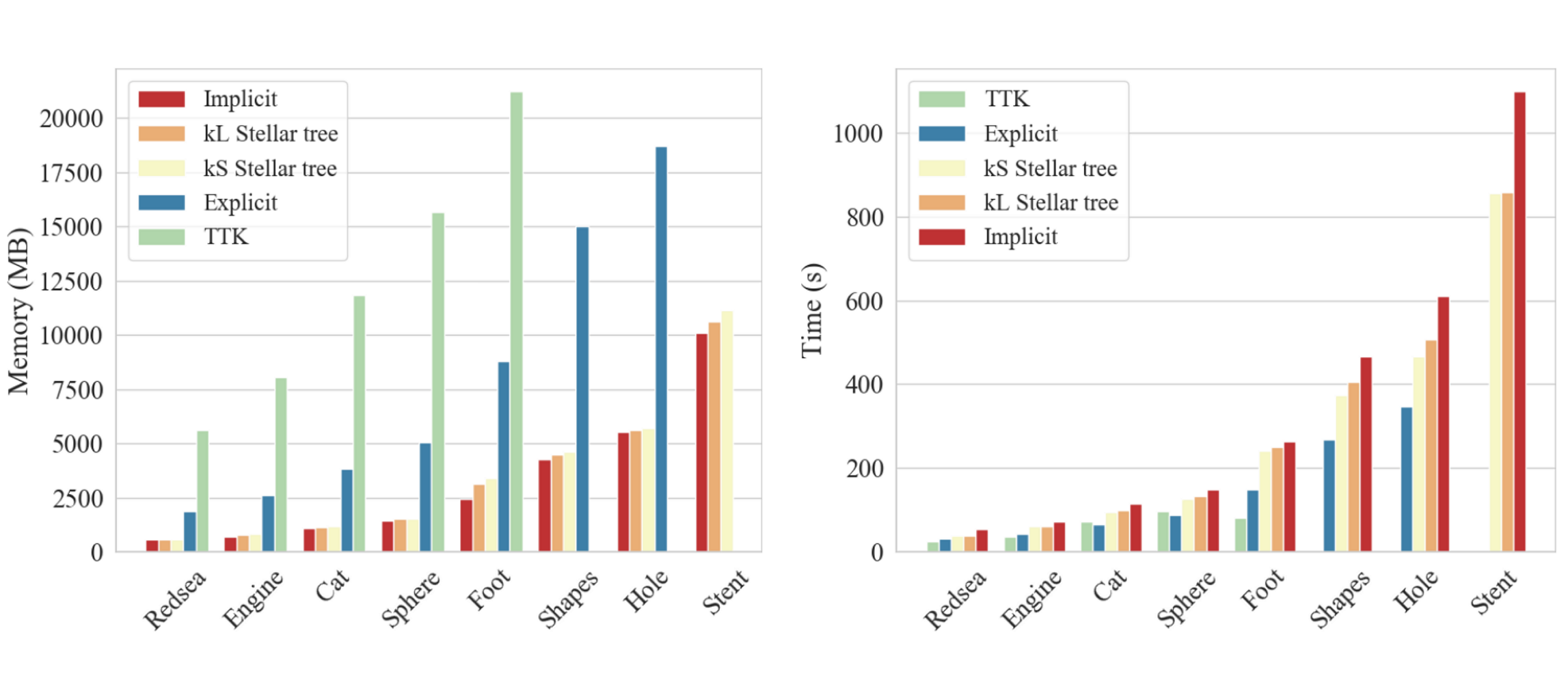
TopoCluster: A Localized Data Structure for Topology-based Visualization
Guoxi Liu, Federico Iuricich, Riccardo Fellegara, and Leila De FlorianiIEEE Transactions on Visualization and Computer Graphics (preprint), 2021.
Abstract
Unstructured data are collections of points with irregular topology, often represented through simplicial meshes, such as triangle and tetrahedral meshes. Whenever possible such representations are avoided in visualization since they are computationally demanding if compared with regular grids. In this work, we aim at simplifying the encoding and processing of simplicial meshes. The paper proposes TopoCluster, a new localized data structure for tetrahedral meshes. TopoCluster provides efficient computation of the connectivity of the mesh elements with a low memory footprint. The key idea of TopoCluster is to subdivide the simplicial mesh into clusters. Then, the connectivity information is computed locally for each cluster and discarded when it is no longer needed. We define two instances of TopoCluster. The first instance prioritizes time efficiency and provides only a modest savings in memory, while the second instance drastically reduces memory consumption up to an order of magnitude with respect to comparable data structures. Thanks to the simple interface provided by TopoCluster, we have been able to integrate both data structures into the existing Topological Toolkit (TTK) framework. As a result, users can run any plugin of TTK using TopoCluster without changing a single line of code.

The Stellar decomposition: A compact representation for simplicial complexes and beyond
Riccardo Fellegara, Kenneth Weiss, and Leila De FlorianiComputers & Graphics, 98 , pages 322-343, 2021.
Abstract
We introduce the Stellar decomposition, a model for efficient topological data structures over a broad range of simplicial and cell complexes. A Stellar decomposition of a complex is a collection of regions indexing the complex’s vertices and cells such that each region has sufficient information to locally reconstruct the star of its vertices, i.e., the cells incident in the region’s vertices. Stellar decompositions are general in that they can compactly represent and efficiently traverse arbitrary complexes with a manifold or non-manifold domain. They are scalable to complexes in high dimension and of large size, and they enable users to easily construct tailored application-dependent data structures using a fraction of the memory required by a corresponding global topological data structure on the complex. # As a concrete realization of this model for spatially embedded complexes, we introduce the Stellar tree, which combines a nested spatial tree with a simple tuning parameter to control the number of vertices in a region. Stellar trees exploit the complex’s spatial locality by reordering vertex and cell indices according to the spatial decomposition and by compressing sequential ranges of indices. Stellar trees are competitive with state-of-the-art topological data structures for manifold simplicial complexes and offer significant improvements for cell complexes and non-manifold simplicial complexes. We conclude with a high-level description of several mesh processing and analysis applications that utilize Stellar trees to process large datasets.
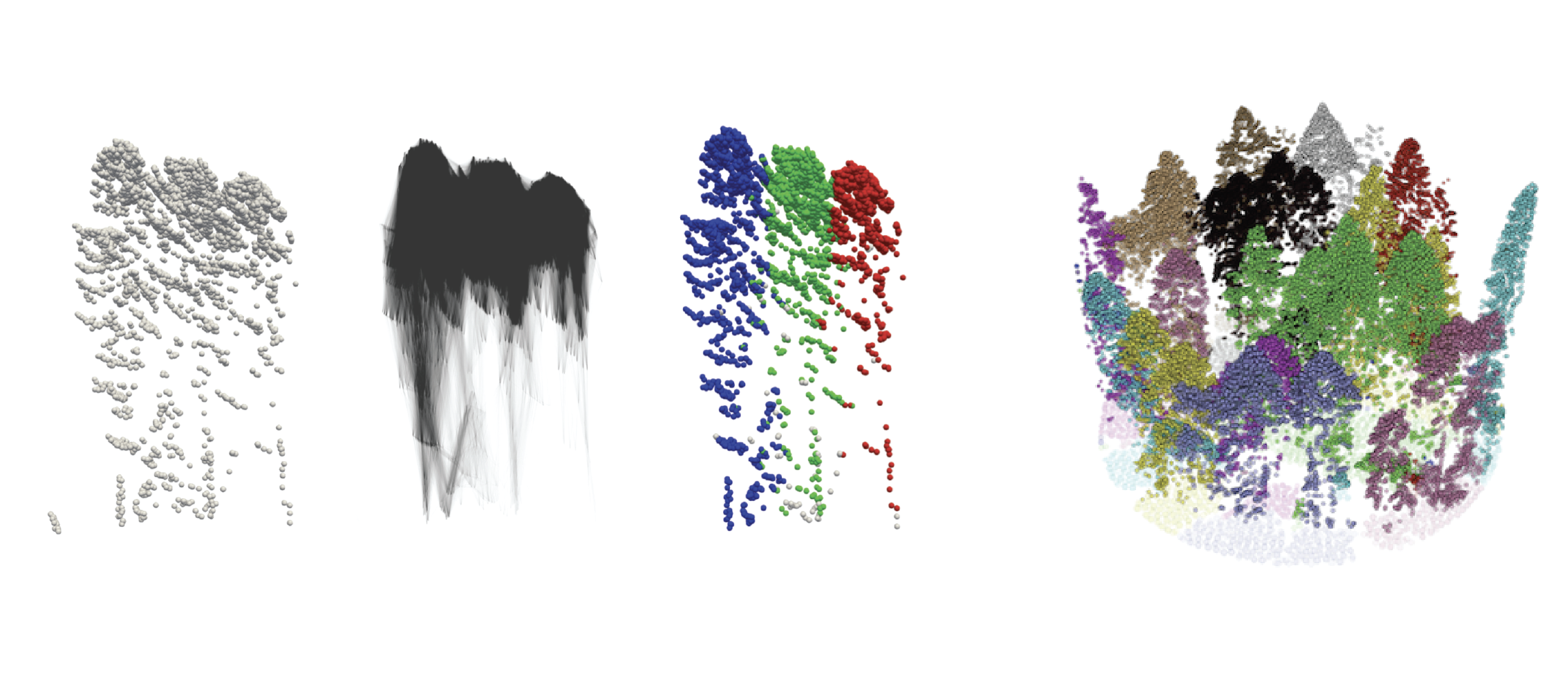
A Persistence-Based Approach for Individual Tree Mapping
Xin Xu, Federico Iuricich, and Leila De FlorianiProceedings of the 28th International Conference on Advances in Geographic Information Systems, pages 191–194, 2021.
Abstract
Light Detection and Ranging (LiDAR) sensors generate dense point clouds that can be used to map forest structures at a high spatial resolution level. In this work, we consider the problem of identifying individual trees in a LiDAR point cloud. Existing techniques generally require intense parameter tuning and user interactions. Our goal is defining an automatic approach capable of providing robust results with minimal user interactions. To this end, we define a segmentation algorithm based on the watershed transform and persistence-based simplification. The proposed algorithm uses a divide-and-conquer technique to split a LiDAR point cloud into regions with uniform density. Within each region, single trees are identified by applying a segmentation approach based on watershed by simulated immersion. Experiments show that our approach performs better than state-of-the-art algorithms on most of the study areas in the benchmark provided by the NEW technologies for a better mountain FORest timber mobilization (NEWFOR) project. Moreover, our approach requires a single (Boolean) parameter. This makes our approach well suited for a wide range of forest analysis applications, including biomass estimation, or field inventory surveys.

Tetrahedral Trees: A Family of Hierarchical Spatial Indexes for Tetrahedral Meshes
Riccardo Fellegara, Leila De Floriani, Paola Magillo, and Kenneth WeissACM Transactions on Spatial Algorithms and Systems, 6 (4), pages 1-34, 2020.
Abstract
We address the problem of performing efficient spatial and topological queries on large tetrahedral meshes with arbitrary topology and complex boundaries. Such meshes arise in several application domains, such as 3D Geographic Information Systems (GISs), scientific visualization, and finite element analysis. To this aim, we propose Tetrahedral trees, a family of spatial indexes based on a nested space subdivision (an octree or a kD-tree) and defined by several different subdivision criteria. We provide efficient algorithms for spatial and topological queries on Tetrahedral trees and compare to state-of-the-art approaches. Our results indicate that Tetrahedral trees are an improvement over R*-trees for querying tetrahedral meshes; they are more compact, faster in many queries, and stable at variations of construction thresholds. They also support spatial queries on more general domains than topological data structures, which explicitly encode adjacency information for efficient navigation but have difficulties with domains with a non-trivial geometric or topological shape.
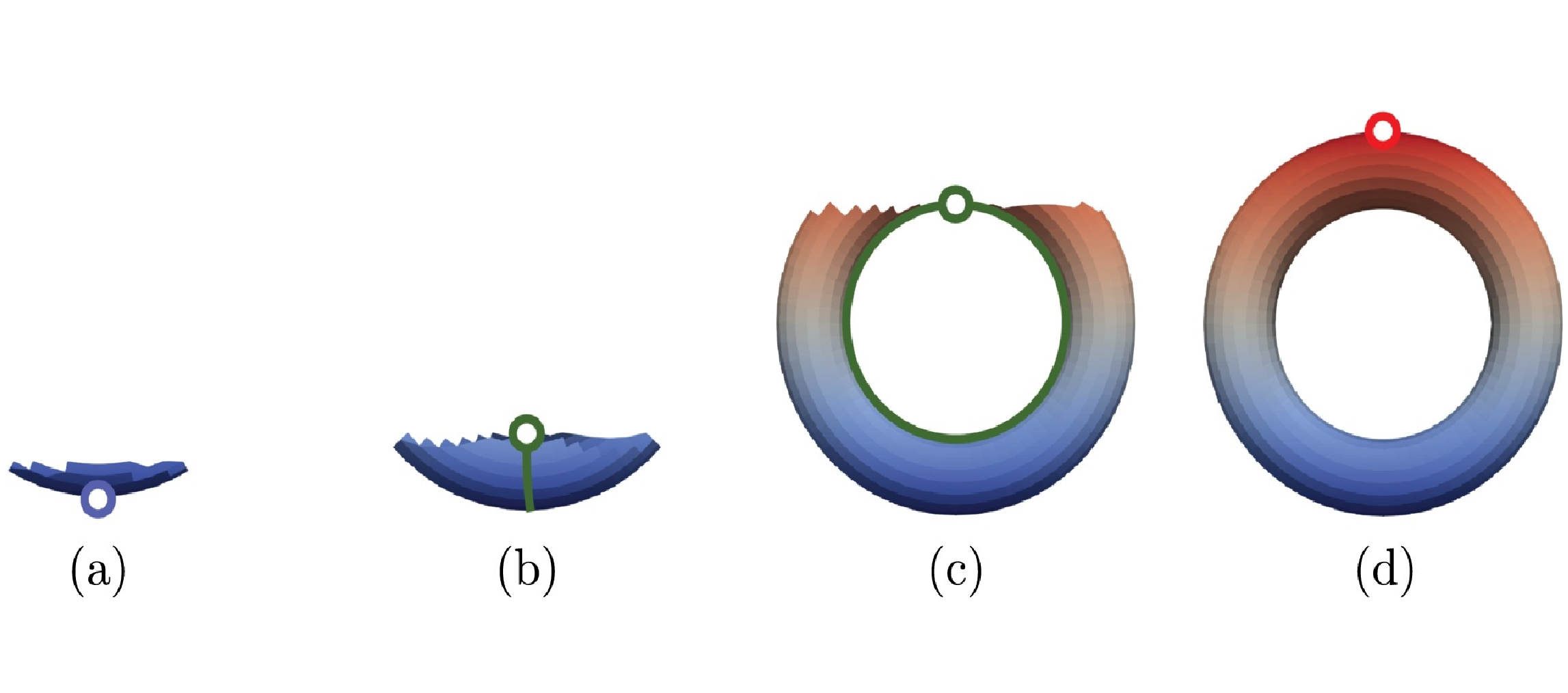
Computing multiparameter persistent homology through a discrete Morse-based approach
Sara Scaramuccia, Federico Iuricich, Leila De Floriani, and Claudia LandiComputational Geometry, 89 , 2020.
Abstract
Persistent homology allows for tracking topological features, like loops, holes and their higher-dimensional analogues, along a single-parameter family of nested shapes. Computing descriptors for complex data characterized by multiple parameters is becoming a major challenging task in several applications, including physics, chemistry, medicine, and geography. Multiparameter persistent homology generalizes persistent homology to allow for the exploration and analysis of shapes endowed with multiple filtering functions. Still, computational constraints prevent multiparameter persistent homology to be a feasible tool for analyzing large size data sets. We consider discrete Morse theory as a strategy to reduce the computation of multiparameter persistent homology by working on a reduced dataset. We propose a new preprocessing algorithm, well suited for parallel and distributed implementations, and we provide the first evaluation of the impact of multiparameter persistent homology on computations.
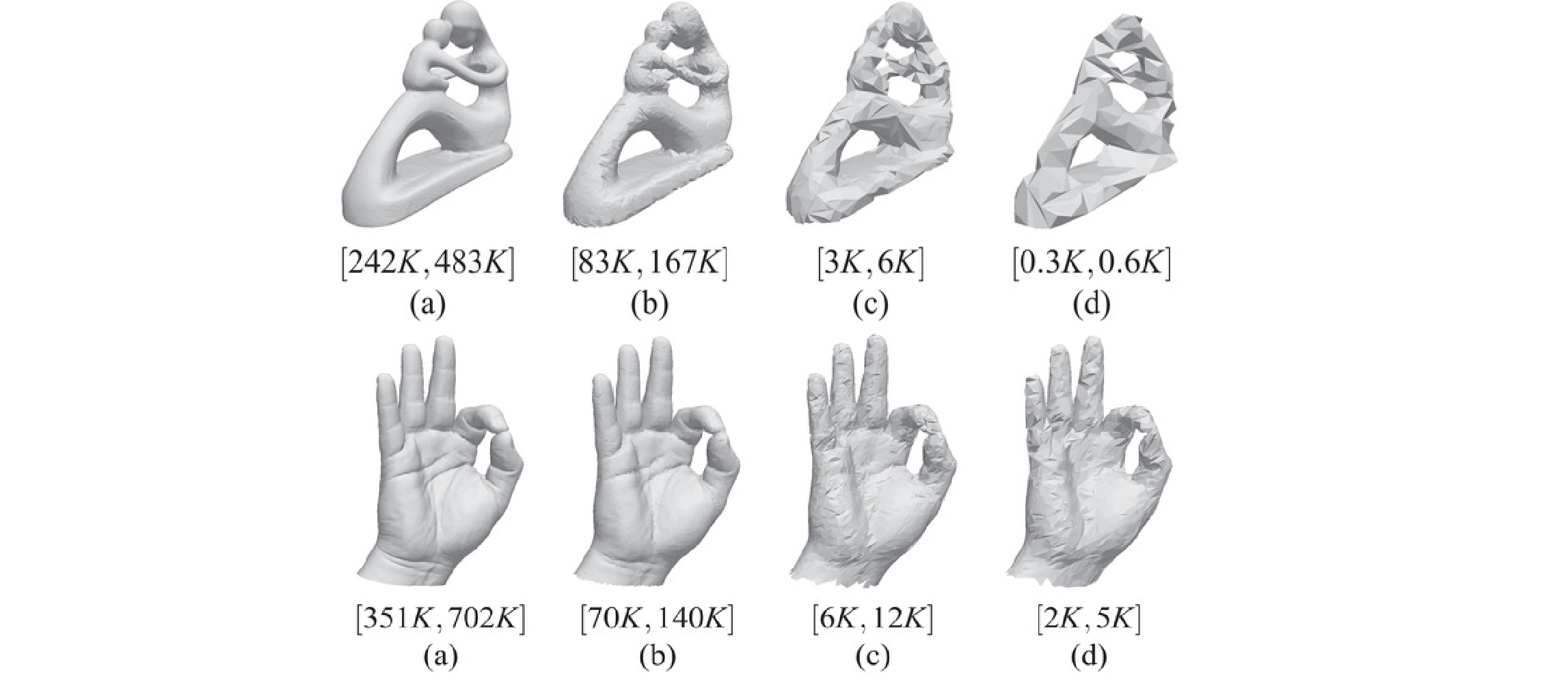
Efficient Homology-Preserving Simplification of High-Dimensional Simplicial Shapes
Riccardo Fellegara, Federico Iuricich, Leila De Floriani, and Ulderico FugacciComputer Graphics Forum, 39 (1), pages 244-259, 2020.
Abstract
Simplicial complexes are widely used to discretize shapes. In low dimensions, a 3D shape is represented by discretizing its boundary surface, encoded as a triangle mesh, or by discretizing the enclosed volume, encoded as a tetrahedral mesh. High-dimensional simplicial complexes have recently found their application in topological data analysis. Topological data analysis aims at studying a point cloud P, possibly embedded in a high-dimensional metric space, by investigating the topological characteristics of the simplicial complexes built on P. Analysing such complexes is not feasible due to their size and dimensions. To this aim, the idea of simplifying a complex while preserving its topological features has been proposed in the literature. Here, we consider the problem of efficiently simplifying simplicial complexes in arbitrary dimensions. We provide a new definition for the edge contraction operator, based on a top-based data structure, with the objective of preserving structural aspects of a simplicial shape (i.e., its homology), and a new algorithm for verifying the link condition on a top-based representation. We implement the simplification algorithm obtained by coupling the new edge contraction and the link condition on a specific top-based data structure, that we use to demonstrate the scalability of our approach.
Simplex and diamond hierarchies: Models and applications
Kenneth Weiss, and Leila De FlorianiEurographics 2010 - State of the Art Reports, 30 (8), pages 2127-2155, 2019.

Computing discrete Morse complexes from simplicial complexes
Ulderico Fugacci, Federico Iuricich, and Leila De FlorianiGraphical Models, 103 , 2019.
Abstract
We consider the problem of efficiently computing a discrete Morse complex on simplicial complexes of arbitrary dimension and very large size. Based on a common graph-based formalism, we analyze existing data structures for simplicial complexes, and we define an efficient encoding for the discrete Morse gradient on the most compact of such representations. We theoretically compare methods based on reductions and coreductions for computing a discrete Morse gradient, proving that the combination of reductions and coreductions produces new mutually equivalent approaches. We design and implement a new algorithm for computing a discrete Morse complex on simplicial complexes. We show that our approach scales very well with the size and the dimension of the simplicial complex also through comparisons with the only existing public-domain algorithm for discrete Morse complex computation. We discuss applications to the computation of multi-parameter persistent homology and of extremum graphs for visualization of time-varying 3D scalar fields.
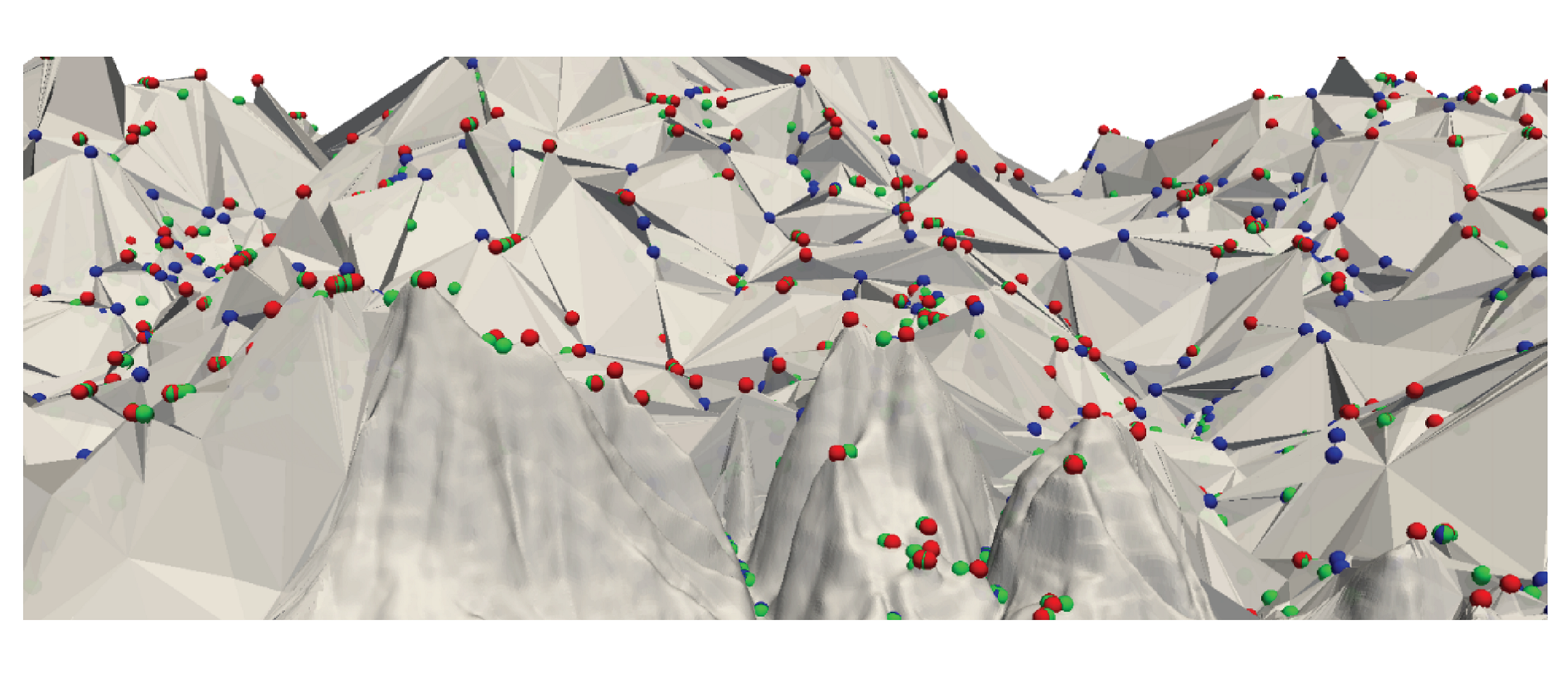
Hierarchical Forman Triangulation: A multiscale model for scalar field analysis
Federico Iuricich, and Leila De FlorianiComputers & Graphics, 66 , pages 113-123, 2017.
Abstract
We consider the problem of analyzing the topology of scalar fields defined on a triangulated shape by using a multi-scale approach, which allows reducing storage costs and computation times, and supports interactive inspection and classification of topological features. We define and implement a multi-scale model that we call a Hierarchical Forman Triangulation (HFT), where a 3D shape or a terrain is discretized as a triangle mesh, and its topology is described by defining a discrete Morse gradient field based on function values given at the vertices of the mesh. We introduce a new edge contraction operator, which does not change the behavior of the gradient flow and does not create new critical points, and we apply it in combination with a topological simplification operator which eliminates critical elements in pair. By combining the two operators in a sequence, we generate the HFT. We discuss and implement a compact encoding for the HFT that has a lower storage cost with respect to the triangle mesh at full resolution. We show the effectiveness of this new hierarchical model by extracting representations of terrains and shapes endowed with a scalar field at different, uniform and variable, scales and by efficiently computing topological features and segmentations.
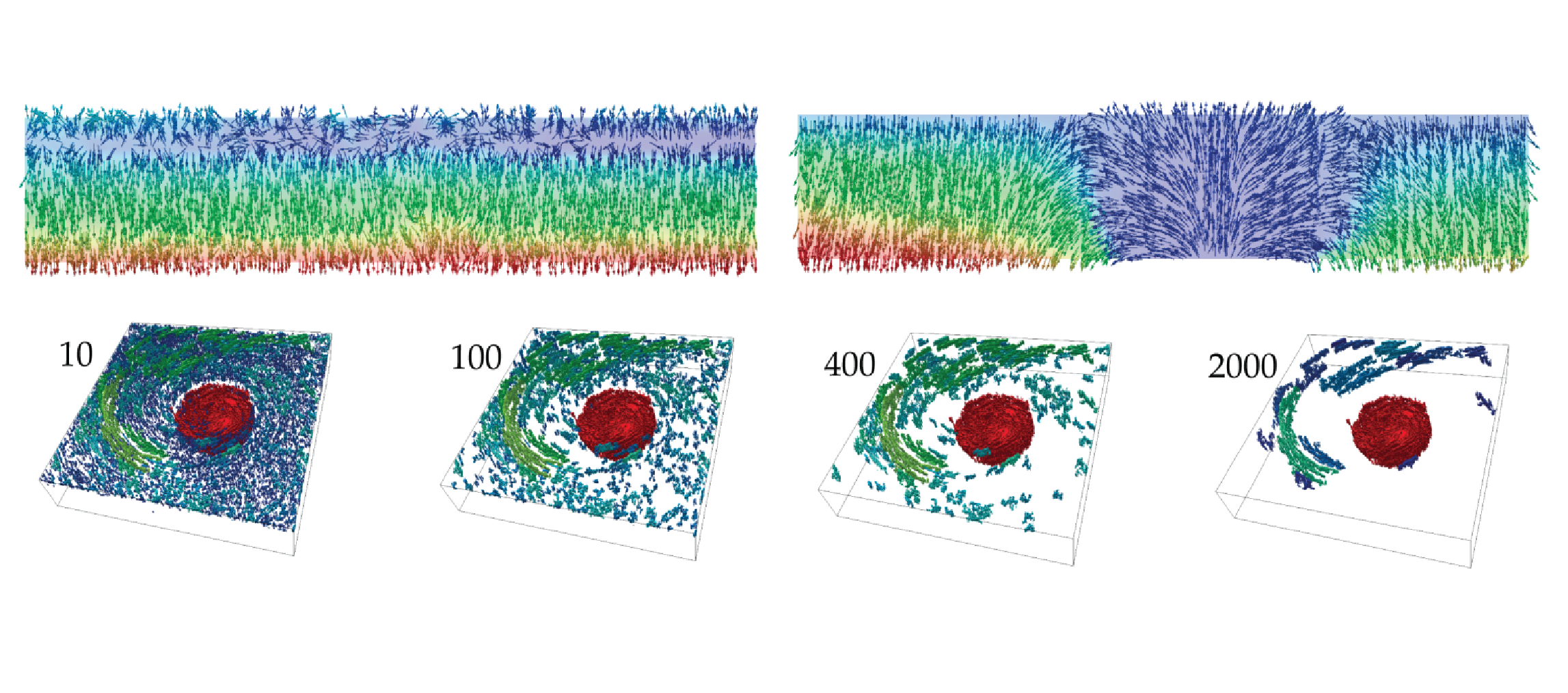
A Discrete Morse-Based Approach to Multivariate Data Analysis
Federico Iuricich, Sara Scaramuccia, Claudia Landi, and Leila De FlorianiSIGGRAPH ASIA 2016 Symposium on Visualization, pages 1-8, 2016.
Abstract
Multivariate data are becoming more and more popular in several applications, including physics, chemistry, medicine, geography, etc. A multivariate dataset is represented by a cell complex and a vector-valued function defined on the complex vertices. The major challenge arising when dealing with multivariate data is to obtain concise and effective visualizations. The usability of common visual elements (e.g., color, shape, size) deteriorates when the number of variables increases. Here, we consider Discrete Morse Theory (DMT) [Forman 1998] for computing a discrete gradient field on a multivariate dataset. We propose a new algorithm, well suited for parallel and distribute implementations. We discuss the importance of obtaining the discrete gradient as a compact representation of the original complex to be involved in the computation of multidimensional persistent homology. Moreover, the discrete gradient field that we obtain is at the basis of a visualization tool for capturing the mutual relationships among the different functions of the dataset.
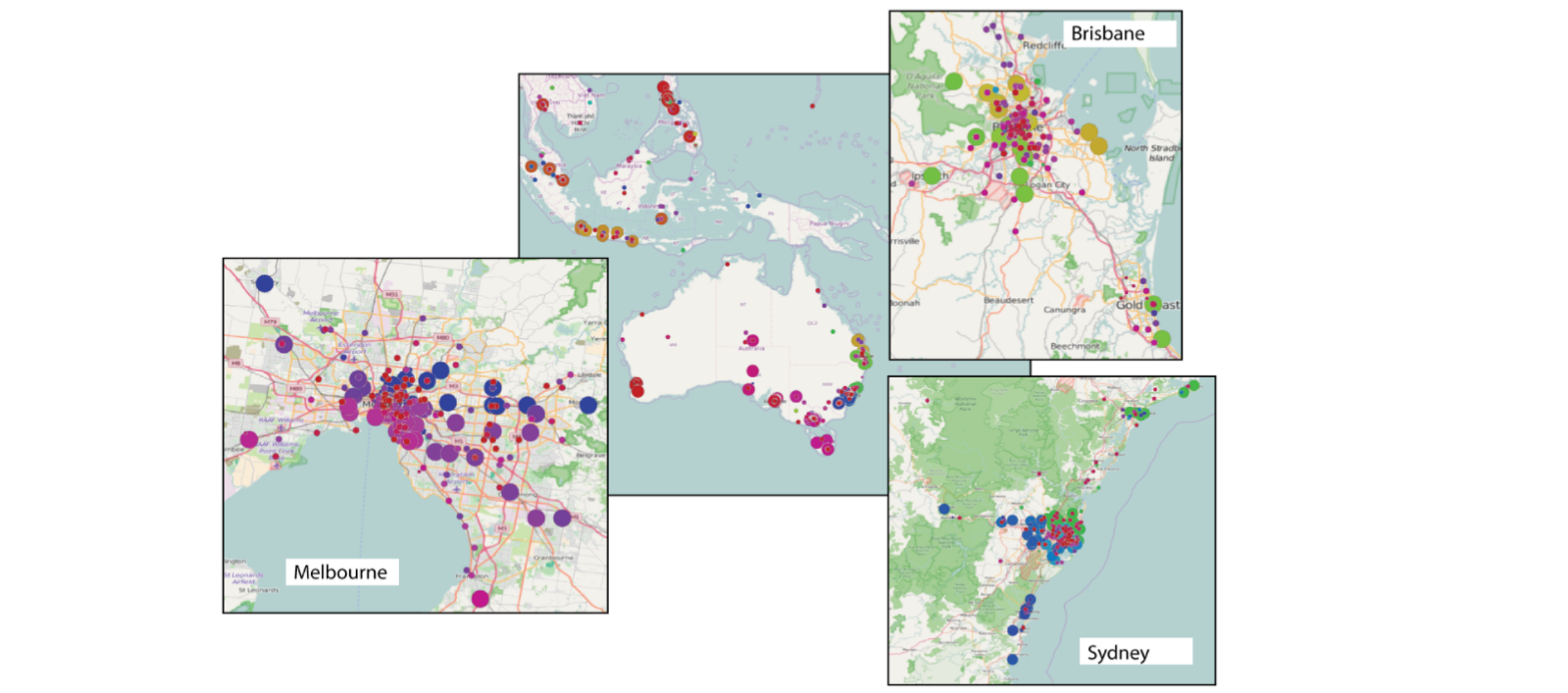
Analysis of Geolocalized Social Networks Based on Simplicial Complexes
Riccardo Fellegara, Ulderico Fugacci, Federico Iuricich, and Leila De FlorianiProceedings of the 9th ACM SIGSPATIAL Workshop on Location-based Social Networks, pages 1-8, 2016.
Abstract
A common issue in network analysis consists in the detection and characterization of the key vertices and communities. To this purpose, visualization tools could be of great help to support domain experts in analyzing this kind of data. However, the size of real networks can seriously affect the practical usage of these tools, thus, requiring the definition of suitable simplification procedures that preserve the core network information. In this work, we focus on geolocalized social networks, and we describe a tool for the analysis of this kind of data based on topological information. Supported by recent trends in network analysis, our approach uses simplicial complexes as a model for social networks. A homology-preserving simplification is used for dealing with the data complexity and for reducing the information to be visualized to the essential. By combining the representation based on simplicial complexes and the simplification tool, we can efficiently retrieve topological information useful for the network analysis. Both the effectiveness and scalability of our approach are experimentally demonstrated.
Homological Shape Analysis Through Discrete Morse Theory
Leila De Floriani, Ulderico Fugacci, and Federico IuricichPerspectives in Shape Analysis, pages 187-209, 2016.
Abstract
Homology and persistent homology are fundamental tools for shape analysis and understanding that recently gathered a lot of interest, in particular for analyzing multidimensional data. In this context, discrete Morse theory, a combinatorial counterpart of smooth Morse theory, provides an excellent basis for reducing computational complexity in homology detection. A discrete Morse complex, computed over a given complex discretizing a shape, drastically reduces the number of cells of the latter while maintaining the same homology. Here, we consider the problem of shape analysis through discrete Morse theory, and we review and analyze algorithms for computing homology and persistent homology based on such theory.
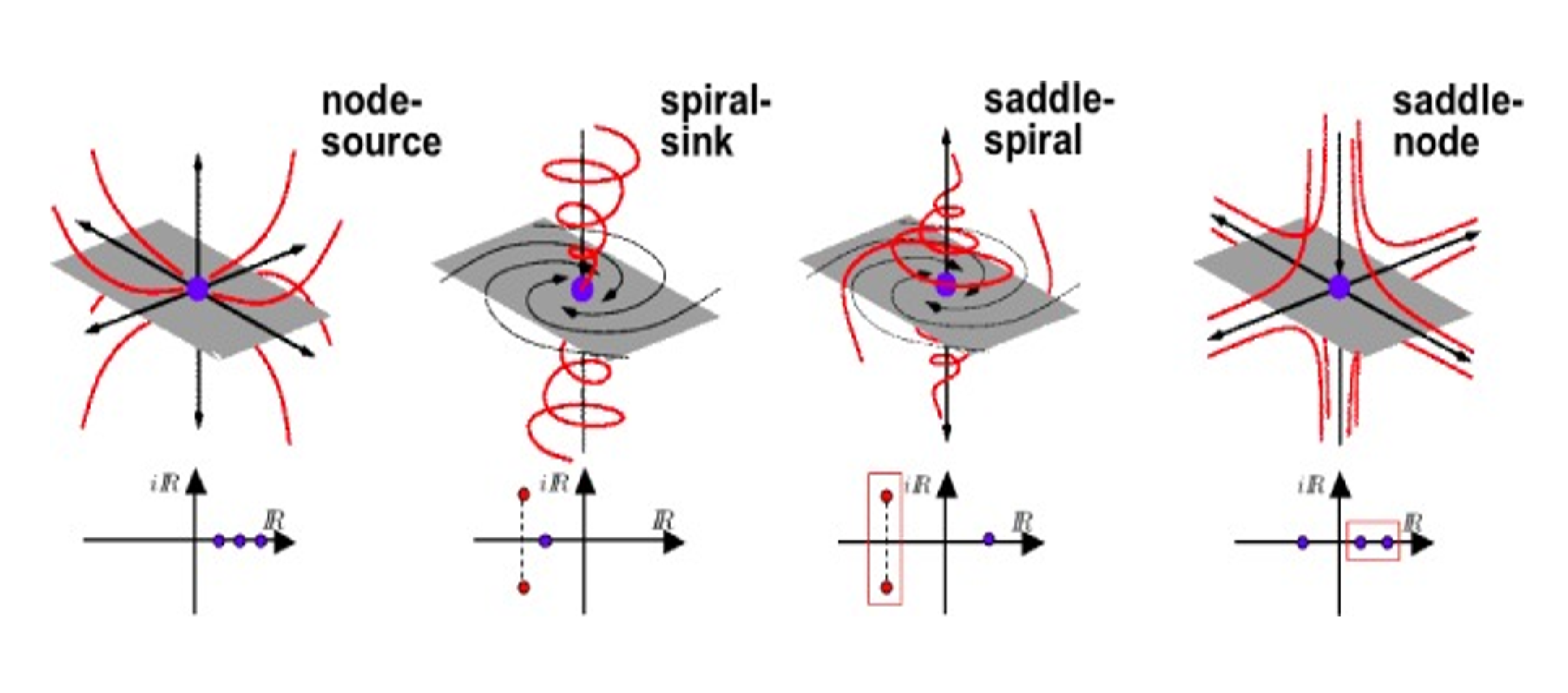
A Survey of Topology-based Methods in Visualization
Christian Heine, Heike Leitte, Mario Hlawitschka, Federico Iuricich, Leila De Floriani, Gerik Scheuermann, Hans Hagen, and Christoph GarthComputer Graphics Forum, 35 , pages 643-667, 2016.
Abstract
This paper presents the state of the art in the area of topology-based visualization. It describes the process and results of an extensive annotation for generating a definition and terminology for the field. The terminology enabled a typology for topological models which is used to organize research results and the state of the art. Our report discusses relations among topological models and for each model describes research results for the computation, simplification, visualization, and application. The paper identifies themes common to subfields, current frontiers, and unexplored territory in this research area.

Computing a discrete Morse gradient from a watershed decomposition
Lidija Comic, Leila De Floriani, Federico Iuricich, and Paola MagilloComputers & Graphics, 58 , pages 43-52, 2016.
Abstract
We consider the problem of segmenting triangle meshes endowed with a discrete scalar function based on the critical points of . The watershed transform induces a decomposition of the domain of function into regions of influence of its minima, called catchment basins. The discrete Morse gradient induced by allows recovering not only catchment basins but also a complete topological characterization of the function and of the shape on which it is defined through a Morse decomposition. Unfortunately, discrete Morse theory and related algorithms assume that the input scalar function has no flat areas, whereas such areas are common in real data and are easily handled by watershed algorithms. We propose here a new approach for building a discrete Morse gradient on a triangulated 3D shape endowed by a scalar function starting from the decomposition of the shape induced by the watershed transform. This allows for treating flat areas without adding noise to the data. Experimental results show that our approach has significant advantages over existing ones, which eliminate noise through perturbation: it is faster and always precise in extracting the correct number of critical elements.
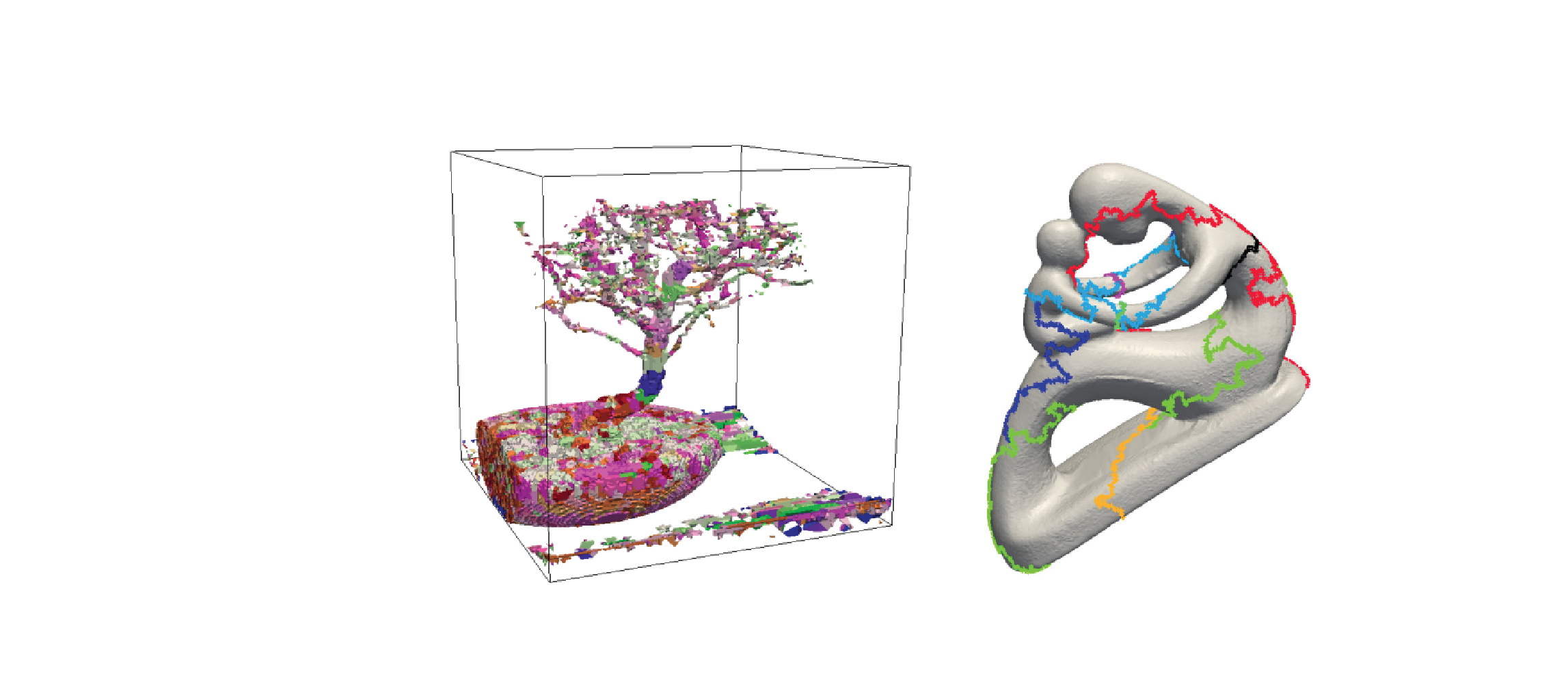
Morse Complexes for Shape Segmentation and Homological Analysis: Discrete Models and Algorithms
Leila De Floriani, Ulderico Fugacci, Federico Iuricich, and Paola MagilloComputer Graphics Forum, 34 , pages 761-785, 2015.
Abstract
Morse theory offers a natural and mathematically-sound tool for shape analysis and understanding. It allows studying the behavior of a scalar function defined on a manifold. Starting from a Morse function, we can decompose the domain of the function into meaningful regions associated with the critical points of the function. Such decompositions, called Morse complexes, provide a segmentation of a shape and are extensively used in terrain modeling and in scientific visualization. Discrete Morse theory, a combinatorial counterpart of smooth Morse theory defined over cell complexes, provides an excellent basis for computing Morse complexes in a robust and efficient way. Moreover, since a discrete Morse complex computed over a given complex has the same homology as the original one, but fewer cells, discrete Morse theory is a fundamental tool for efficiently detecting holes in shapes through homology and persistent homology. In this survey, we review, classify and analyze algorithms for computing and simplifying Morse complexes in the context of such applications with an emphasis on discrete Morse theory and on algorithms based on it.
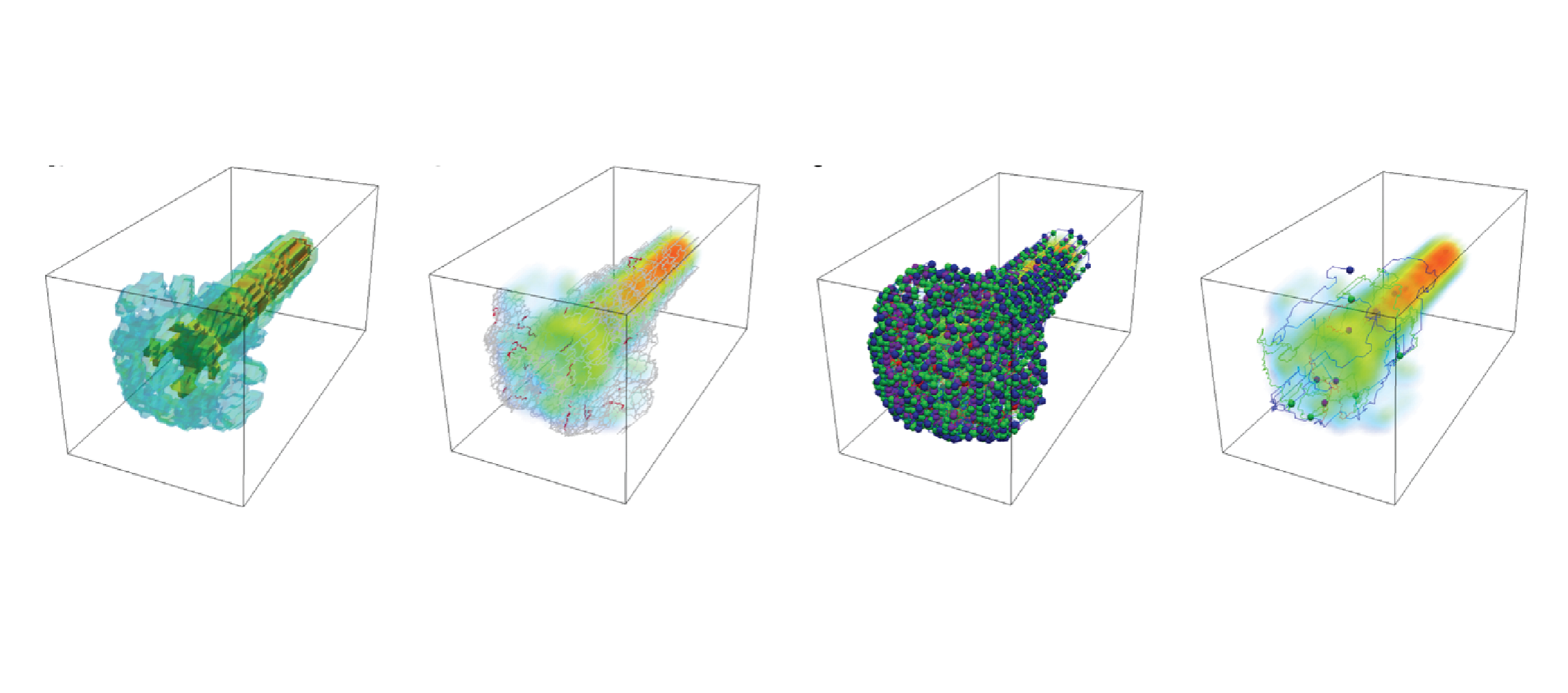
Topologically-Consistent Simplification of Discrete Morse Complex.
Federico Iuricich, Ulderico Fugacci, and Leila De FlorianiComputers & Graphics, 51 , pages 157-166, 2015.
Abstract
We address the problem of simplifying Morse–Smale complexes computed on volume datasets based on discrete Morse theory. Two approaches have been proposed in the literature based on a graph representation of the Morse–Smale complex (explicit approach) and on the encoding of the discrete Morse gradient (implicit approach). It has been shown that this latter can generate topologically-inconsistent representations of the Morse–Smale complex with respect to those computed through the explicit approach. We propose a new simplification algorithm that creates topologically-consistent Morse–Smale complexes and works both with the explicit and the implicit representations. We prove the correctness of our simplification approach, implement it on volume data sets described as unstructured tetrahedral meshes and evaluate its simplification power with respect to the usual Morse simplification algorithm.
Extended version of Ulderico Fugacci, Federico Iuricich, Leila De Floriani (2014). Efficient Computation of Simplicial Homology through Acyclic Matching. 16th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, pages 587-593, 2014.
PDF DOI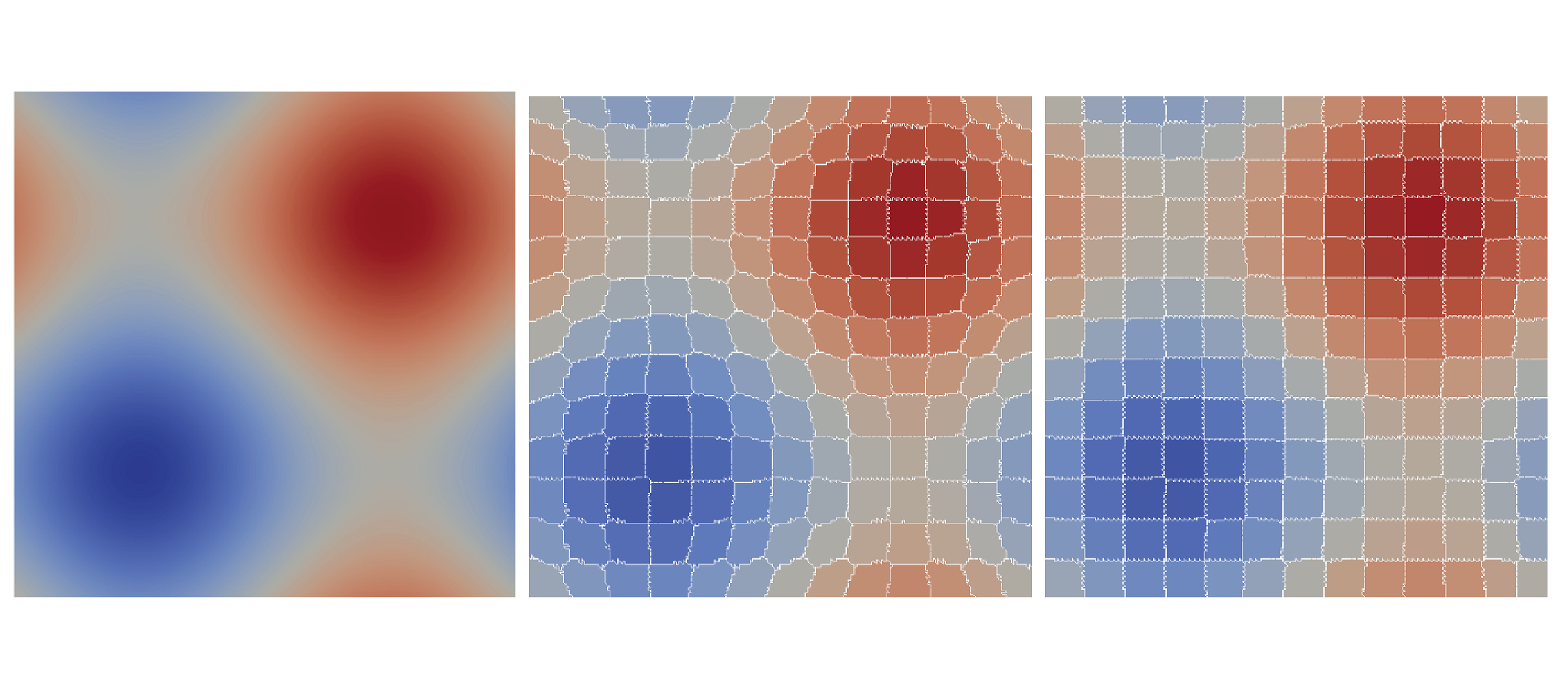
Supertetras: A Superpixel Analog for Tetrahedral Mesh Oversegmentation
Giulia Picciau, Patricio Simari, Federico Iuricich, and Leila De FlorianiImage Analysis and Processing — ICIAP 2015, 9279 , pages 375–386, 2015.
Abstract
Over the past decade, computer vision algorithms have transitioned from relying on the direct, pixel-based representation of images to the use of superpixels, small regions whose boundaries agree with image contours. This intermediate representation improves the tractability of image understanding because it reduces the number of primitives to be taken under consideration from several million to a few hundred. Despite the improvements yielded in the area of image segmentation, the concept of an oversegmentation as an intermediate representation has not been adopted in volumetric mesh processing. We take a first step in this direction, adapting a fast and efficient superpixel algorithm to the tetrahedral mesh case, present results which demonstrate the quality of the output oversegmentation, and illustrate its use in a semantic segmentation application.
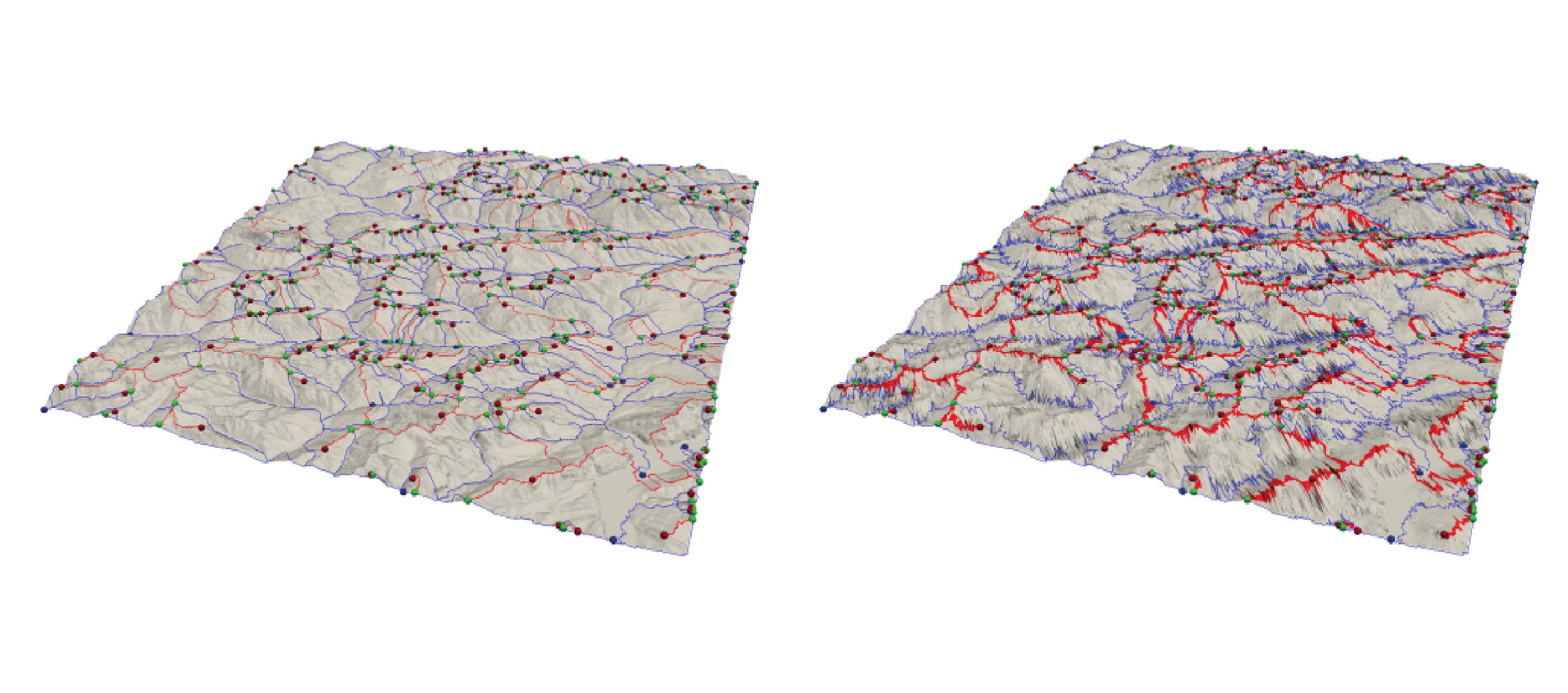
A Combined Geometrical and Topological Simplification Hierarchy for Terrain Analysis
Federico Iuricich, and Leila De FlorianiProceedings of the 22nd ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, pages 493-496, 2014.
Abstract
We consider the problem of modeling a terrain from both a geometric and a morphological point of view for efficient and effective terrain analysis on large data sets. We devise and implement a simplification hierarchy for a triangulated terrain, where the terrain is represented as a triangle mesh and its morphology is described by a discrete Morse gradient field defined on the basis on the elevation values given at the vertices of the mesh. The discrete Morse gradient is attached to the triangles, edges and vertices of the mesh. We define a new edge-contraction operator for the edges of the triangle mesh, which does not change the behavior of the gradient flow and does not create new critical points, and we apply it to the original full-resolution mesh in combination with a topological simplification operator which eliminates critical simplices in pair. We build the simplification hierarchy based on suitably combining such operators and we evaluate it experimentally.
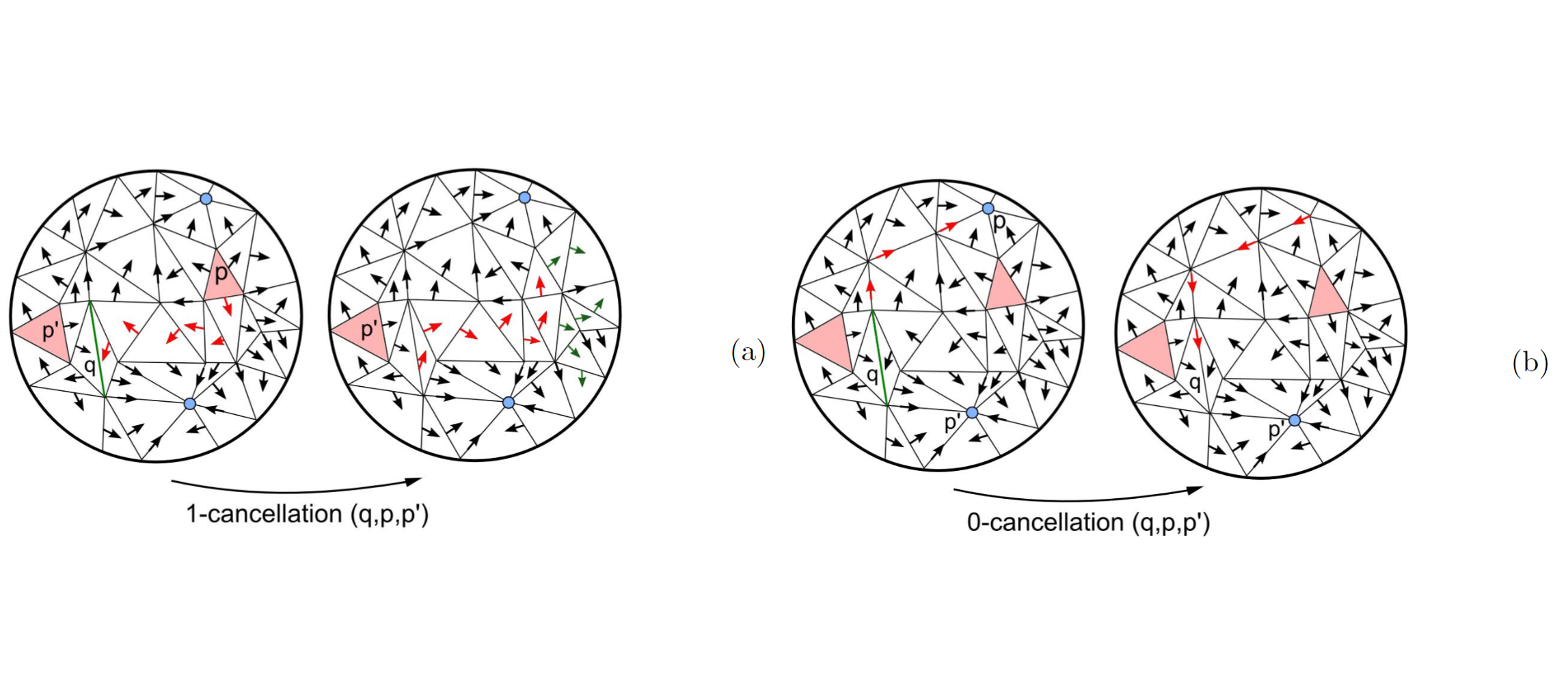
Efficient Computation and Simplification of Discrete Morse Decompositions on Triangulated Terrains
Riccardo Fellegara, Federico Iuricich, Leila De Floriani, and Kenneth WeissProceedings of the 22Nd ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, pages 223-232, 2014.
Abstract
We consider the problem of efficient computing and simplifying Morse complexes on a Triangulated Irregular Network (TIN) based on discrete Morse theory. We develop a compact encoding for the discrete Morse gradient field, defined by the terrain elevation, by attaching it to the triangles of the TIN. This encoding is suitable to be combined with any TIN data structure storing just its vertices and triangles. We show how to compute such gradient field from the elevation values given at the TIN vertices, and how to simplify it effectively in order to reduce the number of critical elements. We demonstrate the effectiveness and scalability of our approach over large terrains by developing algorithms for extracting the cells of the Morse complexes as well as the graph joining the critical elements from the discrete gradient field. We compare implementations of our approach on a widely-used and compact adjacency-based topological data structure for a TIN and on a compact spatio-topological data structure that we have recently developed, the PR-star quadtree.
![Morphological Modeling of Terrains and Volume Data [Book]](/publication/comic-2014-morphological/featured.png)
Morphological Modeling of Terrains and Volume Data [Book]
Lidija Comic, Leila De Floriani, Paola Magillo, and Federico IuricichSpringer, 2014.
Abstract
This book describes the mathematical background behind discrete approaches to morphological analysis of scalar fields, with a focus on Morse theory and on the discrete theories due to Banchoff and Forman. The algorithms and data structures presented are used for terrain modeling and analysis, molecular shape analysis, and for analysis or visualization of sensor and simulation 3D data sets. It covers a variety of application domains including geography, geology, environmental sciences, medicine and biology. The authors classify the different approaches to morphological analysis which are all based on the construction of Morse or Morse-Smale decompositions. They describe algorithms for computing such decompositions for both 2D and 3D scalar fields, including those based on the discrete watershed transform. Also addressed are recent developments in the research on morphological shape analysis, such as simplification operators for Morse and Morse-Smale complexes and their multi-resolution representation. Designed for professionals and researchers involved with modeling and algorithm analysis, Morphological Modeling of Terrains and Volume Data is a valuable resource. Advanced-level students of computer science, mathematics and geography will also find the content very helpful.

Fast and Scalable Mesh Superfacets
Patricio Simari, Giulia Picciau, and Leila De FlorianiComputer Graphics Forum, 33 (7), pages 181-190, 2014.
Abstract
In the field of computer vision, the introduction of a low-level preprocessing step to oversegment images into superpixels - relatively small regions whose boundaries agree with those of the semantic entities in the scene - has enabled advances in segmentation by reducing the number of elements to be labeled from hundreds of thousands, or millions, to a just few hundred. While some recent works in mesh processing have used an analogous oversegmentation, they were not intended to be general and have relied on graph cut techniques that do not scale to current mesh sizes. Here, we present an iterative superfacet algorithm and introduce adaptations of undersegmentation error and compactness, which are well-motivated and principled metrics from the vision community. We demonstrate that our approach produces results comparable to those of the normalized cuts algorithm when evaluated on the Princeton Segmentation Benchmark, while requiring orders of magnitude less time and memory and easily scaling to, and enabling the processing of, much larger meshes.
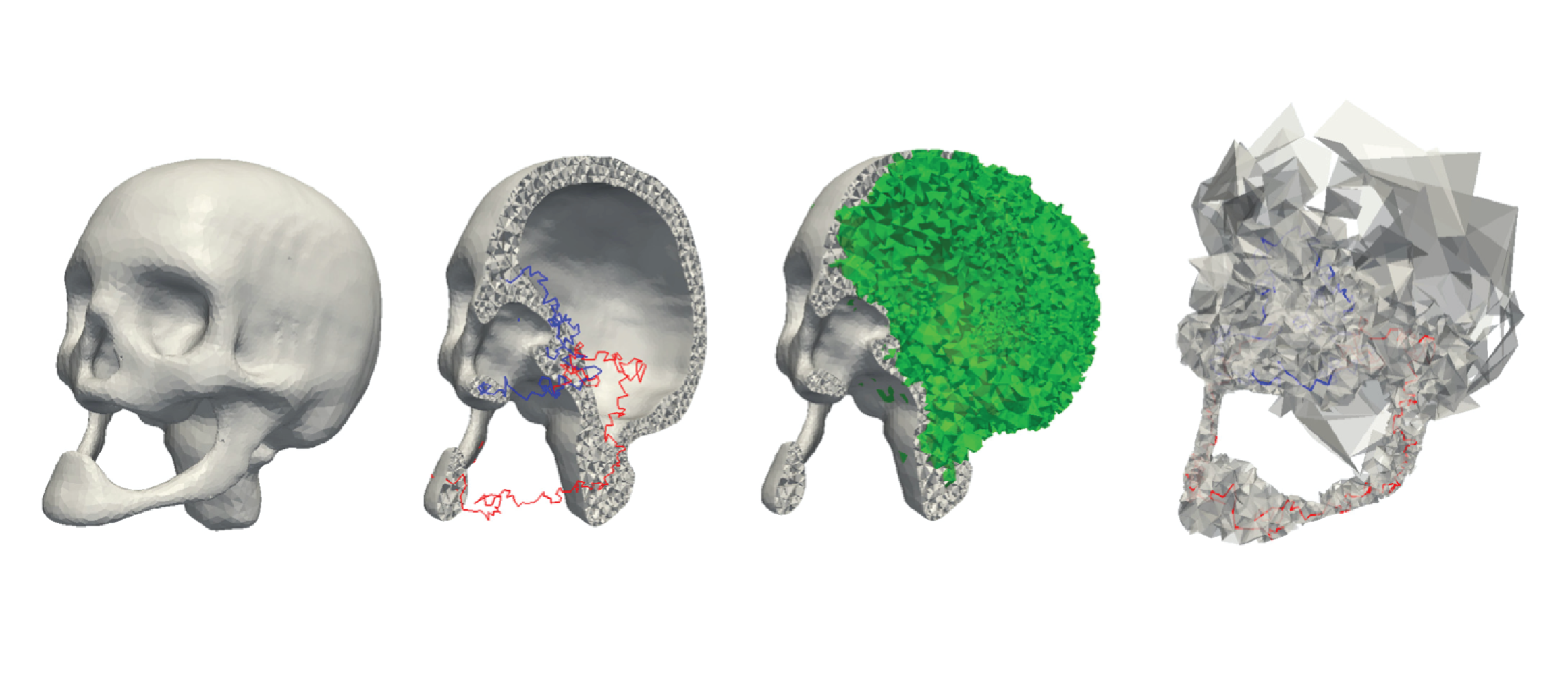
Topological modifications and hierarchical representation of cell complexes in arbitrary dimensions
Lidija Comic, Leila De Floriani, Federico Iuricich, and Ulderico FugacciComputer Vision and Image Understanding, 121 , pages 2-12, 2014.
Abstract
We propose a set of atomic modeling operators for simplifying and refining cell complexes in arbitrary dimensions. Such operators either preserve the homology of the cell complex, or they modify it in a controlled way. We show that such operators form a minimally complete basis for updating cell complexes, and we compare them with various operators previously proposed in the literature. Based on the new operators, we define a hierarchical model for cell complexes, that we call a Hierarchical Cell Complex (HCC), and we discuss its properties. An HCC implicitly encodes a virtually continuous set of complexes obtained from the original complex through the application of our operators. Then, we describe the implementation of a version of the HCC based on the subset of the proposed modeling operators which preserve homology. We apply the homology-preserving HCC to enhance the efficiency in extracting homology generators at different resolutions. To this aim, we propose an algorithm which computes homology generators on the coarsest representation of the original complex, and uses the hierarchical model to propagate them to complexes at any intermediate resolution, and we prove its correctness. Finally, we present experimental results showing the efficiency and effectiveness of the proposed approach.
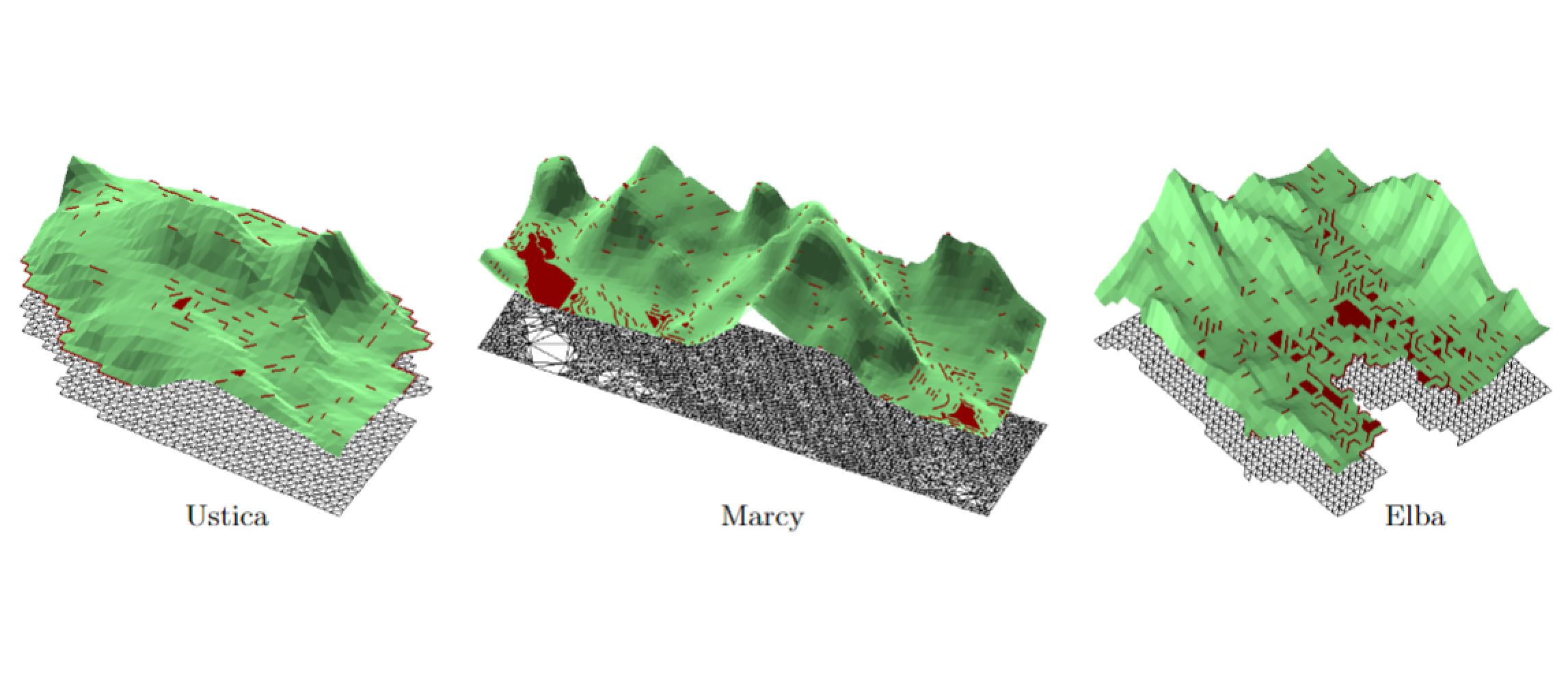
Morphologically-aware elimination of flat edges from a TIN
Paola Magillo, Leila De Floriani, and Federico IuricichProceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, pages 244-253, 2013.
Abstract
We propose a new technique for eliminating flat edges from a Triangulated Irregular Network (TIN) in a morphologically consistent way. The algorithm is meant to be a preprocessing step for performing morphological computations on a terrain. Terrain morphology is rooted in Morse theory for smooth functions. Segmentation algorithms have been defined for TINs, mostly based on discrete versions of Morse theory, and under the assumption that the terrain model does not include flat edges. On the other hand, flat edges often occur in real data, and thus either they are eliminated through data perturbation, or the segmentation algorithms must be able to deal with them. In both cases, the resulting Morse segmentations are highly affected by the presence of flat edges. The new technique we propose provides a better solution, as it preserves the set of maxima and minima of the original terrain, and improves consistency among the terrain decompositions produced by different segmentation algorithms.
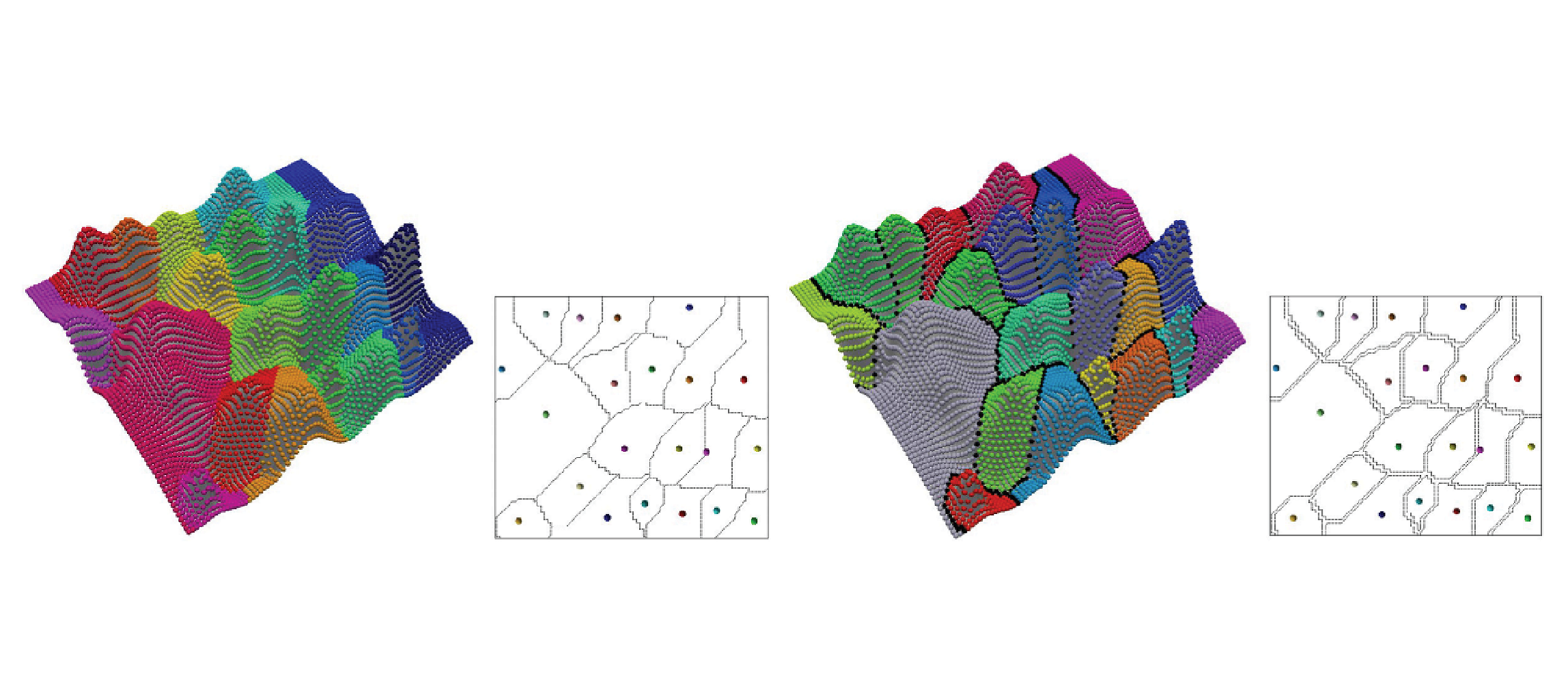
Discrete Morse versus Watershed Decompositions of Tessellated Manifolds
Leila De Floriani, Federico Iuricich, Paola Magillo, and Patricio D. SimariImage Analysis and Processing - ICIAP 2013, 8157 , pages 339-348, 2013.
Abstract
With improvements in sensor technology and simulation methods, datasets are growing in size, calling for the investigation of efficient and scalable tools for their analysis. Topological methods, able to extract essential features from data, are a prime candidate for the development of such tools. Here, we examine an approach based on discrete Morse theory and compare it to the well-known watershed approach as a means of obtaining Morse decompositions of tessellated manifolds endowed with scalar fields, such as triangulated terrains or tetrahedralized volume data. We examine the theoretical aspects as well as present empirical results based on synthetic and real-world data describing terrains and 3D scalar fields. We will show that the approach based on discrete Morse theory generates segmentations comparable to the watershed approach while being theoretically sound, more efficient with regard to time and space complexity, easily parallelizable, and allowing for the computation of all descending and ascending i-manifolds and the topological structure of the two Morse complexes.
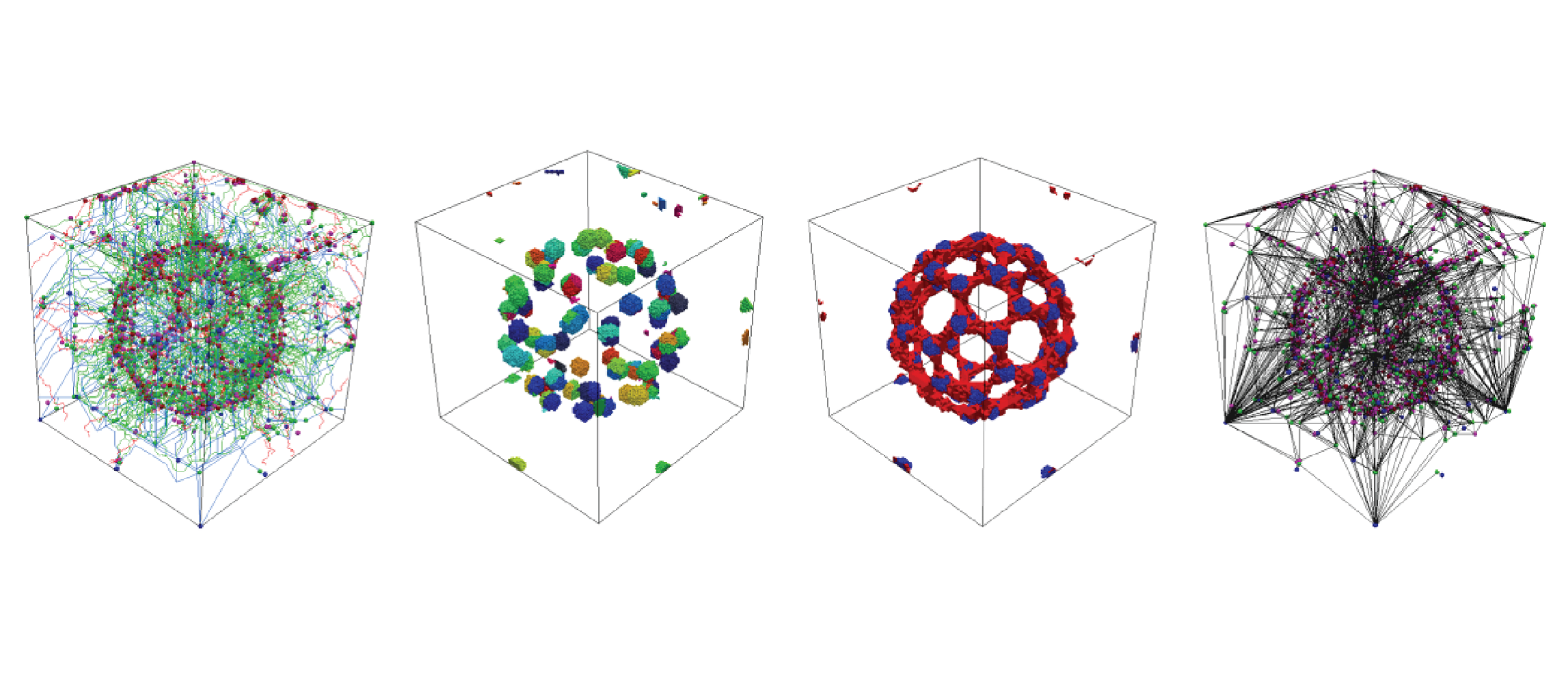
A Primal/Dual Representation for Discrete Morse Complexes on Tetrahedral Meshes
Kenneth Weiss, Federico Iuricich, Riccardo Fellegara, and Leila De FlorianiComputer Graphics Forum, 32 (3), pages 361-370, 2013.
Abstract
We consider the problem of computing discrete Morse and Morse-Smale complexes on an unstructured tetrahedral mesh discretizing the domain of a 3D scalar field. We use a duality argument to define the cells of the descending Morse complex in terms of the supplied (primal) tetrahedral mesh and those of the ascending complex in terms of its dual mesh. The Morse-Smale complex is then described combinatorially as collections of cells from the intersection of the primal and dual meshes. We introduce a simple compact encoding for discrete vector fields attached to the mesh tetrahedra that is suitable for combination with any topological data structure encoding just the vertices and tetrahedra of the mesh. We demonstrate the effectiveness and scalability of our approach over large unstructured tetrahedral meshes by developing algorithms for computing the discrete gradient field and for extracting the cells of the Morse and Morse-Smale complexes. We compare implementations of our approach on an adjacency-based topological data structure and on the PR-star octree, a compact spatio-topological data structure.
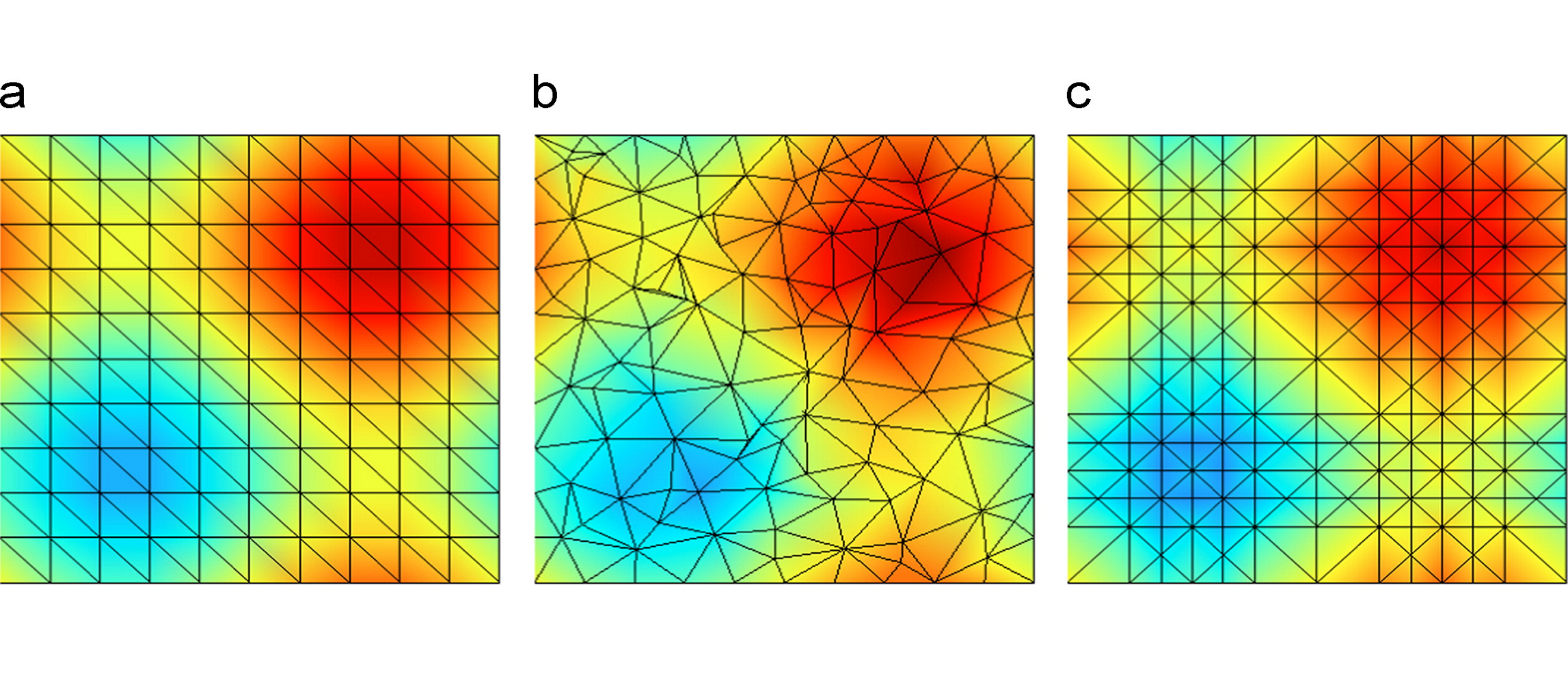
Generalized Extrinsic Distortion and Applications
Patricio Simari, Leila De Floriani, Federico Iuricich, and Mohammed M. MesmoudiComputers & Graphics, 37 (6), pages 582-588, 2013.
Abstract
Curvature is a key feature in shape analysis and its estimation on discrete simplicial complexes benefits many geometry processing applications. However, its study has mostly remained focused on 2D manifolds and computationally practical extensions to higher dimensions remain an active area of computer science research. We examine the existing notions of distortion, an analog of curvature in the discrete setting, and classify them into two categories: intrinsic and extrinsic, depending on whether they use the interior or the dihedral angles of the tessellation. We then propose a generalization of extrinsic distortion to ce:italic> D /ce:italic> D and derive a weighting that can be used to compute mean curvature on tessellated hypersurfaces. We analyze the behavior of the operator on 3-manifolds in 4D and compare it to the well-known Laplace–Beltrami operator using ground truth hypersurfaces defined by functions of three variables, and a segmentation application, showing it to behave as well or better while being intuitively simple and easy to implement.

Simplification Operators on a Dimension-Independent Graph-Based Representation of Morse Complexes
Lidija Comic, Leila De Floriani, and Federico IuricichMathematical Morphology and Its Applications to Signal and Image Processing, 7883 , pages 13-24, 2013.
Abstract
Ascending and descending Morse complexes are defined by the critical points and integral lines of a scalar field f defined on a manifold M. They induce a subdivision of M into regions of uniform gradient flow, thus providing a compact description of the topology of M and of the behavior of f over M. We represent the ascending and descending Morse complexes of f as a graph, that we call the Morse incidence graph (MIG). We have defined a simplification operator on the graph-based representation, which is atomic and dimension-independent, and we compare this operator with a previous approach to the simplification of 3D Morse complexes based on the cancellation operator. We have developed a simplification algorithm based on a simplification operator, which operates on the MIG, and we show results from this implementation as well as comparisons with the cancellation operator in 3D.
Research Projects
Modular data structures for meshes and simplicial complexes
Efficient mesh data structures play a fundamental role in a broad range of mesh processing applications, in computer graphics, geometric modeling, scientific visualization, geospatial data science and finite element analysis. Although simple problems can be easily modeled on small low dimensional meshes, phenomena of interest might occur only on much larger meshes and in higher dimensions, as for simplicial complexes describing the shape of high-dimensional point clouds. In our research, we have developed a new data model for meshes and simplicial complexes, that we call a Stellar decomposition, which combines the encoding of minimal mesh connectivity information with a clustering mechanism on the vertices and cells of the mesh. Unlike combinatorial data structures, which explicitly encode the connectivity among cells of the mesh, this general approach has been shown to support scalability with size and dimension, and efficient processing of fundamental connectivity queries in a distributed fashion. Based on this model, we have developed new efficient representations for tetrahedral meshes endowed with a scalar field for the analysis and visualization of 3D scalar fields, and for arbitrary simplicial complexes. We have also devised a new and highly efficient decimation approach based on a Stellar decomposition, which simplifies large simplicial complexes by their homological properties.
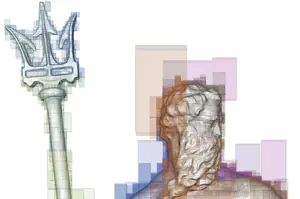
Efficient terrain analysis and processing on a decomposition-based data structure
Triangulated Irregular Network (TIN) is a widely-used model for representing terrain surface, especially when the input dataset is distributed irregularly. When using TINs to represent large terrains, the major challenges are the high storage and time costs. To address these issues, we introduce a family of decomposition-based data structures, named Terrain trees family, for encoding TINs. The compact design and local analysis strategy enable the analysis and processing of large TINs on a single local machine. New terrain analysis methods, including topological analysis and morphological analysis have been developed on Terrain trees. These methods are implemented as an open-source library named Terrain trees library (TTL). Despite the highly efficient data structure, managing large TINs on local machines remains challenging, particularly for complex analyses or simulations. Mesh simplification methods are commonly applied to reduce TIN sizes to enable downstream processing. However, these simplification methods can modify the topology of the underlying terrain in an uncontrolled manner, which affects the results of terrain analysis applications. To address this issue, a topology-aware mesh simplification method based on Terrain trees is proposed. The proposed method is further accelerated by being extended to a parallel computing environment. This project also applies Terrain trees and TTL to a real-world application, the sea ice topography. Studying sea ice topography is crucial as it enhances our ability to monitor sea ice volume changes and to comprehend sea ice processes. Besides, timely and precise assessments of sea ice dynamics are critical in the context of climate change and its impacts on polar regions. TIN-based surface models are employed to represent the sea ice surface, and methods are developed for extracting important sea ice topographic features, such as density, regions without measurements, roughness, and pressure ridge structures, from TINs.

Tree mapping and reconstruction from aerial and terrestrial LiDAR data through topology-based techniques
Light Detection and Ranging (LiDAR) techniques have dramatically enhanced our ability to characterize forest structures remotely by acquiring 3D point cloud samplings of forest shapes. Extracting individual trees from the forests plays a critical role in the automated processing pipeline of forest point cloud analysis. However, there is still a lack of automated, efficient, and easy-to-use approaches available to identify and extract individual trees in a forest point cloud. This is mainly due to inconsistent point cloud quality, diverse forest structure, and complicated plant morphology. Most existing methods require intensive parameter tuning, time-consuming user interactions, and external information (i.e., allometric function). In this reserach, we consider the problem of extracting single-tree point clouds from input forest point clouds. We propose two novel Topology-based Tree Segmentation (TTS) approaches, namely TTS-ALS and TTS-TLS, for airborne and terrestrial laser scanning data analysis, respectively. TTS algorithms are plug-and-play by nature and controlled by at most one parameter, ensuring user-friendliness. The implemented TTS software tools can extract single trees from 3D point clouds on various forest types, including conifer trees, broadleaf deciduous forests, and evergreen subtropical trees. By moving from single-time LiDAR point cloud data to multi-date point clouds, which are scanned from the same forest at different times, we will also segment and analyze LiDAR point clouds over-time.

Continuous terrain modeling and analysis through implicit neural representations
Digital terrain models (DTMs) are pivotal in remote sensing, cartography, and landscape management, requiring accurate surface representation and topological information restoration. While topology analysis traditionally relies on smooth manifolds, the absence of an easy-to-use continuous surface model for a large terrain results in a preference for discrete meshes. Structural representation based on topology provides a succinct surface description, laying the foundation for many terrain analysis applications. However, on discrete meshes, numerical issues emerge, and complex algorithms are designed to handle them. This research aims to bring the context of terrain data analysis back to the continuous world and uses implicit neural representation (INR) approach for modeling high-resolution terrain continuously and differentiably. Our model has superior surface fitting accuracy, effective topological feature retrieval, and various topographical feature extraction that are implemented over this compact representation in parallel.

Distributed topology-based terrain analysis using Apache Spark
High-quality and extensive LiDAR data support and enhance large-scale terrain modeling. Triangulated Irregular Networks (TINs) are widely used representations for modeling a terrain topology, even on irregularly sampled raw data. One major application of TINs is for the efficient extraction of morphological features. Morphological features are defined by critical points on the terrain (such as peaks, valleys, and ridges) and their connectivity, which are fundamental for terrain analysis in many applications, including urban analysis, forest monitoring, and bathymetric simulations. However, existing data structures for TINs experience a prohibitive memory cost when computing the connectivity of the terrain and when extracting its morphological features, especially on large datasets comprising billions of points. We address this problem by proposing a novel framework for efficient and scalable topological analysis of large TINs using Apache Spark. The proposed framework, called Morse- Spark, is based on a novel data structure for encoding a TIN on distributed frameworks and integrates distributed algorithms inspired by Discrete Morse theory to extract connectivity relations, critical points, and their regions of influence. To prove the effectiveness and scalability of such a framework, we compare Morse-Spark against three well-established software libraries for topology-based TIN analysis. Our experimental evaluation with real-world TINs shows that Morse-Spark can effectively handle datasets at least 20 times bigger than any other approach for topological analysis.

Visualization, Data Quality, and Scale in Composite Bathymetric Data Generalization
Contemporary bathymetric data collection techniques are capable of collecting sub-meter resolution data to ensure full seafloor-bottom coverage for safe navigation as well as to support other various scientific uses of the data. Moreover, bathymetry data are becoming increasingly available. Datasets are compiled from these sources and used to update Electronic Navigational Charts (ENCs), the primary medium for visualizing the seafloor for navigation purposes, whose usage is mandatory on Safety Of Life At Sea (SOLAS) regulated vessels. However, these high-resolution data must be generalized for products at scale, an active research area in automated cartography. Algorithms that can provide consistent results while reducing production time and costs are increasingly valuable to organizations operating in time-sensitive environments. This is particularly the case in digital nautical cartography, where updates to bathymetry and locations of dangers to navigation need to be disseminated as quickly as possible. Therefore, this research covers the development of cartographic constraint-based generalization algorithms operating on both Digital Surface Model (DSM) and Digital Cartographic Model (DCM) representations of multi-source composite bathymetric data to produce navigationally-ready datasets for use at scale. Similarly, many coastal data analysis applications utilize unstructured meshes for representing terrains due to the adaptability, which allows for better conformity to the shoreline and bathymetry. Finer resolution along narrow geometric features, steep gradients, and submerged channels, and coarser resolution in other areas, reduces the size of the mesh while maintaining a comparable accuracy in subsequent processing. Generally, the mesh is constructed a priori for the given domain and elevations are interpolated to the nodes of the mesh from a predefined digital elevation model. Mesh simplification is a technique used in computer graphics to reduce the complexity of a mesh or surface model while preserving features such as shape, topology, and geometry. This technique can be used to mitigate issues related to processing performance by reducing the number of elements composing the mesh, thus increasing efficiency. The primary challenge is finding a balance between the level of generalization, preservation of specific characteristics relevant to the intended use of the mesh, and computational efficiency. Despite the potential usefulness of mesh simplification for reducing mesh size and complexity while retaining morphological details, there has been little investigation regarding the application of these techniques specifically to Bathymetric Surface Models (BSMs), where additional information such as vertical uncertainty can help guide the process. Toward this effort, this research also explores the effects of BSM mesh simplification on a coastal ocean model forced by tides in New York Harbor.

Geospatial Data Representation and Analysis through the Stellar Decomposition
Check details of: Geospatial Data Representation and Analysis through the Stellar Decomposition
Software
FG_Multi: library for computing a discrete gradient on multivariate data
FG_Multi is a library to compute a discrete gradient on multiparameter filtrations, i.e., filtrations defined by a vector-valued function. It can compute a Forman gradient on a simplicial complex (up to 3 dimensions) with multiple scalar values defined at its vertices. This library uses an incidence-based data structure for compactly encoding the relations among vertices, edges, and triangles. The computation of the Forman gradient relies on homotopic expansion.
The source code and additional information can be found on
GitHub.
References:
(1) A Discrete Morse-Based Approach to Multivariate Data Analysis
by Federico Iuricich, Sara Scaramuccia, Claudia Landi, and Leila De Floriani in SIGGRAPH ASIA 2016 Symposium on Visualization, pages 1-8, 2016.
(2) Computing multiparameter persistent homology through a discrete Morse-based approach
by Sara Scaramuccia, Federico Iuricich, Leila De Floriani, and Claudia Landi in Computational Geometry, 89, 2020.

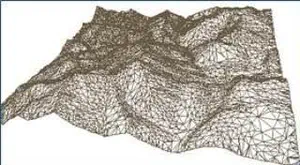
Terrain Trees library: a tool for efficient and scalable terrain mesh processing
Terrain Trees Library (TTL) is a library for terrain analysis based on a new scalable data structure named Terrain trees. Terrain trees are a new in-core family of spatial indexes for the representation and analysis of Triangulated Irregular Networks (TINs). TTL contains a kernel for connectivity and spatial queries, and modules for extracting morphological features, including edge and triangle slopes, roughness, curvature. It also contains modules for extracting topological structures, like critical point, critical net, watershed segmentation, based on the discrete Morse gradient, and a technique for multivariate data visualization, which enables the analysis of multiple scalar fields defined on the same terrain. In addition to analysis operators, TTL includes a module for efficient topology-aware TIN simplification. It can reduce the size of a TIN while maintaining the topology of the underlying terrain. A parallel version of the simplification algorithm based on OpenMP is also included in TTL.
The source code and additional information can be found on
GitHub.
References:
(1) Terrain trees: a framework for representing, analyzing and visualizing triangulated terrains
by Riccardo Fellegara, Federico Iuricich, Yunting Song, and Leila De Floriani in GeoInformatica (preprint), 2022.
(2) Efficient topology-aware simplification of large triangulated terrains
by Yunting Song, Riccardo Fellegara, Federico Iuricich, and Leila De Floriani, Proceedings of the 29th International Conference on Advances in Geographic Information Systems, pages 576–587, 2021.
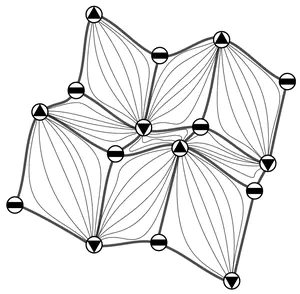
Stellar Trees Library
The Stellar Trees library is a C++ framework for performing efficient topological queries on simplicial and non-simplicial meshes. It provides a scalable and compact representation that encodes the minimal information to locally reconstruct the topological connectivity of its indexed elements. This provides the flexibility to efficiently construct the optimal data structures to solve the task at hand using a fraction of the memory required for a corresponding topological data structure on the global mesh. The efficiency of the Stellar library increases with the execution of successive queries, as the construction costs of these runtime data structures are amortized over multiple accesses while processing each node. For a description of the required libraries for building the library, the compilation process, the run-time options and of the supported input format, please refer to the readme file available in the repository archive.
The source code and additional information can be found on
GitHub.
Reference: The Stellar decomposition: A compact representation for simplicial complexes and beyond
by Riccardo Fellegara, Kenneth Weiss, and Leila De Floriani in Computers & Graphics, 98, pages 322-343, 2021.
Tetrahedral Trees
The Tetrahedral Trees library is a tool for efficient spatial and topological queries on large tetrahedral meshes with arbitrary topology and complex boundaries, which arise in several application domains, such as 3D Geographic Information Systems (GISs), scientific visualization, and finite element analysis. The library is based on Tetrahedral trees, a family of spatial indexes based on a nested space subdivision (an octree or a kD-tree) and defined by several different subdivision criteria. The library contains efficient algorithms for spatial and topological queries on Tetrahedral trees. For a description of the required libraries for building the library, the compilation process, the run-time options and of the supported input format, please refer to the github page of the repository listed above.
The source code and additional information can be found on
GitHub.
Reference: Tetrahedral Trees: A Family of Hierarchical Spatial Indexes for Tetrahedral Meshes
by Riccardo Fellegara, Leila De Floriani, Paola Magillo, and Kenneth Weiss in ACM Transactions on Spatial Algorithms and Systems, 6 (4), pages 1-34, 2020.
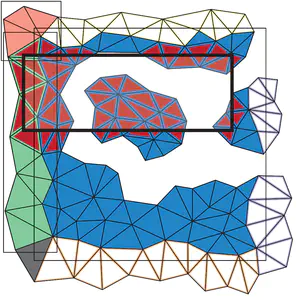
LibTri: Terrain Modeling and Analysis based on the IA data structure
The LibTri library includes the implementation of the Indexed data structure with Adjacencies (IA data structure) for the representation of triangle meshes and functions for terrain analysis based on the IA data structure. The IA data structure is a triangle-based data structure that encodes the vertices and the triangles of the mesh. It also explicitly encodes, for each triangle, the indexes in the triangle table of its three bounding vertices, and for each vertex, the index of one triangle incident in the vertex. This enables the efficient retrieval of all connectivity relations. The functions supported by the LibTri library include state-of-the-art estimators for slope and curvature for triangulated surfaces (Triangulated Irregular Networks - TINs), and for the extraction of critical points from a TIN. The source code and additional information can be found on GitHub. This implementation has been used as a baseline method in the reference paper.
The source code and additional information can be found on
GitHub.
Reference:
Terrain trees: a framework for representing, analyzing and visualizing triangulated terrains
by Riccardo Fellegara, Federico Iuricich, Yunting Song, and Leila De Floriani in GeoInformatica (preprint), 2022.
ICT - Introduction to Computational Topology
The ICT - Introduction to Computational Topology is a web-based user-guide on computational topology equipped with interactive examples to facilitate the comprehension of the notions at the of such theory. Currently the guide presents a description of persistent homology.
The source code and additional information can be found on
GitHub.
Moreover, an interactive guide to Persistent Topology can be found on
GitHub.
Referece: Persistent Homology: a Step-by-Step Introduction for Newcomers
by Ulderico Fugacci, Sara Scaramuccia, Federico Iuricich, and Leila De Floriani in Smart Tools and Apps for Graphics - Eurographics Italian Chapter Conference, 2016.
Forman Gradient 2D
The Forman Gradient 2D is a comprehensive library for computing a Forman Gradient on triangle meshes. The library provides all the basic functions for encoding a triangle mesh and a scalar function defined on its vertices (both provided in input) and for computing a Forman gradient on it. Two different methods have been implemented. The first one is based on homotopic expansion and the second one uses an input watershed segmentation to avoid spurious critical simplices. Additional functions are furnished for computing the cells of the discrete Morse complex and for producing output files to be visualized in Paraview. The library is composed of two main parts. The first one provides all the basic functions for managing the triangle mesh (LibMesh). The second part provides the functions for computing the Forman gradient and the Morse cells (LibForman).
The source code and additional information can be found on
GitHub.
References:
(1) Computing a discrete Morse gradient from a watershed decomposition
by Lidija Comic, Leila De Floriani, Federico Iuricich, and Paola Magill in Computers & Graphics, 58, 43-52, 2016.
(2) A primal/dual representation for discrete Morse complexes on tetrahedral meshes
by Kenneth Weiss, Federico Iuricich, Riccardo Fellegara, and Leila De Floriani in Computer Graphics Forum, 32 (3), 361-370, 2013.

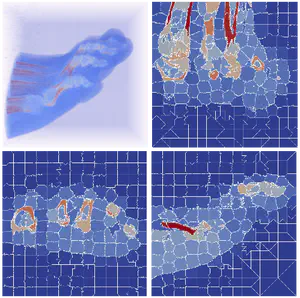
Supertetras
The Supertetras is a C++ tool for computing an oversegmentation of a tetrahedral mesh. The tool extends the state-of-the-art superpixel algorithm to tetrahedral mesh representations with scalar fields defined over their vertices. The segmentation process is based on the k-means algorithm, and thus consists of an initialization step followed by a centroid update and a classification steps, with the latter two steps repeated until convergence.
The source code and additional information can be found on
GitHub.
Reference: Supertetras: A Superpixel Analog for Tetrahedral Mesh Oversegmentation
by Giulia Picciau, Patricio Simari, Federico Iuricich, and Leila De Floriani in Image Analysis and Processing — ICIAP 2015, 9279, pages 375–386, 2015.
Superfacets-2D
The Superfacets-2D is a C++ tool for segmenting the boundary of triangulated 3D shapes into patches by extending the idea of superpixel to triangle meshes. The tool computes oversegmentations of triangle meshes based on a k-means style approach using shortest-path distances over the face graph of the mesh. Its algorithm can be subdivided into three high-level steps: 1) initialization, 2) update of segment centers, and 3) classification of triangles, where steps 2) and 3) are alternately repeated until convergence. By using a bounded expansion strategy in the reclassification step, our approach obtains a log-linear complexity, enabling the segmentation of large meshes (with several million triangles) where applying normalized cuts or other such cut-based approaches would be intractable.
The source code and additional information can be found on
GitHub.
Reference: Fast and Scalable Mesh Superfacets
by Patricio Simari, Giulia Picciau, and Leila De Floriani in Computer Graphics Forum, 33 (7), pages 181-190, 2014.
