Software

FG_Multi is a library to compute a discrete gradient on multiparameter filtrations, i.e., filtrations defined by a vector-valued function. It can compute a Forman gradient on a simplicial complex (up to 3 dimensions) with multiple scalar values defined at its vertices. This library uses an incidence-based data structure for compactly encoding the relations among vertices, edges, and triangles. The computation of the Forman gradient relies on homotopic expansion. The source code and additional information can be found on GitHub.
References:
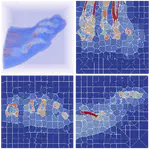
(1) A Discrete Morse-Based Approach to Multivariate Data Analysis by Federico Iuricich, Sara Scaramuccia, Claudia Landi, and Leila De Floriani in SIGGRAPH ASIA 2016 Symposium on Visualization, pages 1-8, 2016.
(2) Computing multiparameter persistent homology through a discrete Morse-based approach by Sara Scaramuccia, Federico Iuricich, Leila De Floriani, and Claudia Landi in Computational Geometry, 89, 2020.

Terrain Trees Library (TTL) is a library for terrain analysis based on a new scalable data structure named Terrain trees. Terrain trees are a new in-core family of spatial indexes for the representation and analysis of Triangulated Irregular Networks (TINs). TTL contains a kernel for connectivity and spatial queries, and modules for extracting morphological features, including edge and triangle slopes, roughness, curvature. It also contains modules for extracting topological structures, like critical point, critical net, watershed segmentation, based on the discrete Morse gradient, and a technique for multivariate data visualization, which enables the analysis of multiple scalar fields defined on the same terrain. In addition to analysis operators, TTL includes a module for efficient topology-aware TIN simplification. It can reduce the size of a TIN while maintaining the topology of the underlying terrain. A parallel version of the simplification algorithm based on OpenMP is also included in TTL. The source code and additional information can be found on GitHub.
References:
(1) Terrain trees: a framework for representing, analyzing and visualizing triangulated terrains by Riccardo Fellegara, Federico Iuricich, Yunting Song, and Leila De Floriani in GeoInformatica (preprint), 2022.
(2) Efficient topology-aware simplification of large triangulated terrains by Yunting Song, Riccardo Fellegara, Federico Iuricich, and Leila De Floriani, Proceedings of the 29th International Conference on Advances in Geographic Information Systems, pages 576–587, 2021.

The Stellar Trees library is a C++ framework for performing efficient topological queries on simplicial and non-simplicial meshes. It provides a scalable and compact representation that encodes the minimal information to locally reconstruct the topological connectivity of its indexed elements. This provides the flexibility to efficiently construct the optimal data structures to solve the task at hand using a fraction of the memory required for a corresponding topological data structure on the global mesh. The efficiency of the Stellar library increases with the execution of successive queries, as the construction costs of these runtime data structures are amortized over multiple accesses while processing each node. For a description of the required libraries for building the library, the compilation process, the run-time options and of the supported input format, please refer to the readme file available in the repository archive. The source code and additional information can be found on GitHub.
Reference: The Stellar decomposition: A compact representation for simplicial complexes and beyond by Riccardo Fellegara, Kenneth Weiss, and Leila De Floriani in Computers & Graphics, 98, pages 322-343, 2021.

The Tetrahedral Trees library is a tool for efficient spatial and topological queries on large tetrahedral meshes with arbitrary topology and complex boundaries, which arise in several application domains, such as 3D Geographic Information Systems (GISs), scientific visualization, and finite element analysis. The library is based on Tetrahedral trees, a family of spatial indexes based on a nested space subdivision (an octree or a kD-tree) and defined by several different subdivision criteria. The library contains efficient algorithms for spatial and topological queries on Tetrahedral trees. For a description of the required libraries for building the library, the compilation process, the run-time options and of the supported input format, please refer to the github page of the repository listed above. The source code and additional information can be found on GitHub.
Reference: Tetrahedral Trees: A Family of Hierarchical Spatial Indexes for Tetrahedral Meshes by Riccardo Fellegara, Leila De Floriani, Paola Magillo, and Kenneth Weiss in ACM Transactions on Spatial Algorithms and Systems, 6 (4), pages 1-34, 2020.

The LibTri library includes the implementation of the Indexed data structure with Adjacencies (IA data structure) for the representation of triangle meshes and functions for terrain analysis based on the IA data structure. The IA data structure is a triangle-based data structure that encodes the vertices and the triangles of the mesh. It also explicitly encodes, for each triangle, the indexes in the triangle table of its three bounding vertices, and for each vertex, the index of one triangle incident in the vertex. This enables the efficient retrieval of all connectivity relations. The functions supported by the LibTri library include state-of-the-art estimators for slope and curvature for triangulated surfaces (Triangulated Irregular Networks - TINs), and for the extraction of critical points from a TIN. The source code and additional information can be found on GitHub. This implementation has been used as a baseline method in the reference paper. The source code and additional information can be found on GitHub.
Reference: Terrain trees: a framework for representing, analyzing and visualizing triangulated terrains by Riccardo Fellegara, Federico Iuricich, Yunting Song, and Leila De Floriani in GeoInformatica (preprint), 2022.

The ICT - Introduction to Computational Topology is a web-based user-guide on computational topology equipped with interactive examples to facilitate the comprehension of the notions at the of such theory. Currently the guide presents a description of persistent homology.
The source code and additional information can be found on GitHub. Moreover, an interactive guide to Persistent Topology can be found on GitHub.
Referece: Persistent Homology: a Step-by-Step Introduction for Newcomers by Ulderico Fugacci, Sara Scaramuccia, Federico Iuricich, and Leila De Floriani in Smart Tools and Apps for Graphics - Eurographics Italian Chapter Conference, 2016.

The Forman Gradient 2D is a comprehensive library for computing a Forman Gradient on triangle meshes. The library provides all the basic functions for encoding a triangle mesh and a scalar function defined on its vertices (both provided in input) and for computing a Forman gradient on it. Two different methods have been implemented. The first one is based on homotopic expansion and the second one uses an input watershed segmentation to avoid spurious critical simplices. Additional functions are furnished for computing the cells of the discrete Morse complex and for producing output files to be visualized in Paraview. The library is composed of two main parts. The first one provides all the basic functions for managing the triangle mesh (LibMesh). The second part provides the functions for computing the Forman gradient and the Morse cells (LibForman). The source code and additional information can be found on GitHub.
References:
(1) Computing a discrete Morse gradient from a watershed decomposition by Lidija Comic, Leila De Floriani, Federico Iuricich, and Paola Magill in Computers & Graphics, 58, 43-52, 2016.
(2) A primal/dual representation for discrete Morse complexes on tetrahedral meshes by Kenneth Weiss, Federico Iuricich, Riccardo Fellegara, and Leila De Floriani in Computer Graphics Forum, 32 (3), 361-370, 2013.

The Supertetras is a C++ tool for computing an oversegmentation of a tetrahedral mesh. The tool extends the state-of-the-art superpixel algorithm to tetrahedral mesh representations with scalar fields defined over their vertices. The segmentation process is based on the k-means algorithm, and thus consists of an initialization step followed by a centroid update and a classification steps, with the latter two steps repeated until convergence.
The source code and additional information can be found on GitHub.
Reference: Supertetras: A Superpixel Analog for Tetrahedral Mesh Oversegmentation by Giulia Picciau, Patricio Simari, Federico Iuricich, and Leila De Floriani in Image Analysis and Processing — ICIAP 2015, 9279, pages 375–386, 2015.

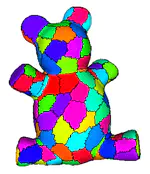
The Superfacets-2D is a C++ tool for segmenting the boundary of triangulated 3D shapes into patches by extending the idea of superpixel to triangle meshes. The tool computes oversegmentations of triangle meshes based on a k-means style approach using shortest-path distances over the face graph of the mesh. Its algorithm can be subdivided into three high-level steps: 1) initialization, 2) update of segment centers, and 3) classification of triangles, where steps 2) and 3) are alternately repeated until convergence. By using a bounded expansion strategy in the reclassification step, our approach obtains a log-linear complexity, enabling the segmentation of large meshes (with several million triangles) where applying normalized cuts or other such cut-based approaches would be intractable.
The source code and additional information can be found on GitHub.
Reference: Fast and Scalable Mesh Superfacets by Patricio Simari, Giulia Picciau, and Leila De Floriani in Computer Graphics Forum, 33 (7), pages 181-190, 2014.