The Stellar decomposition: A compact representation for simplicial complexes and beyond
Abstract
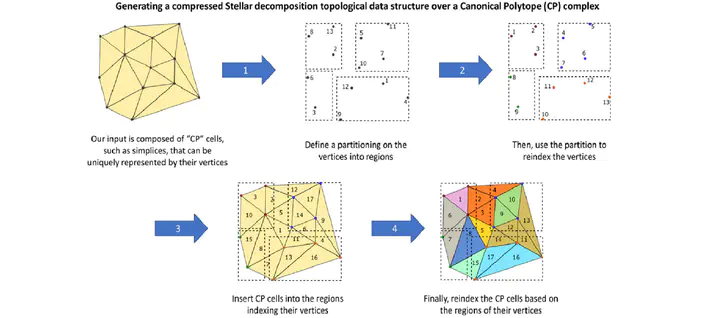
We introduce the Stellar decomposition, a model for efficient topological data structures over a broad range of simplicial and cell complexes. A Stellar decomposition of a complex is a collection of regions indexing the complex’s vertices and cells such that each region has sufficient information to locally reconstruct the star of its vertices, i.e., the cells incident in the region’s vertices. Stellar decompositions are general in that they can compactly represent and efficiently traverse arbitrary complexes with a manifold or non-manifold domain. They are scalable to complexes in high dimension and of large size, and they enable users to easily construct tailored application-dependent data structures using a fraction of the memory required by a corresponding global topological data structure on the complex. # As a concrete realization of this model for spatially embedded complexes, we introduce the Stellar tree, which combines a nested spatial tree with a simple tuning parameter to control the number of vertices in a region. Stellar trees exploit the complex’s spatial locality by reordering vertex and cell indices according to the spatial decomposition and by compressing sequential ranges of indices. Stellar trees are competitive with state-of-the-art topological data structures for manifold simplicial complexes and offer significant improvements for cell complexes and non-manifold simplicial complexes. We conclude with a high-level description of several mesh processing and analysis applications that utilize Stellar trees to process large datasets.