Abstract
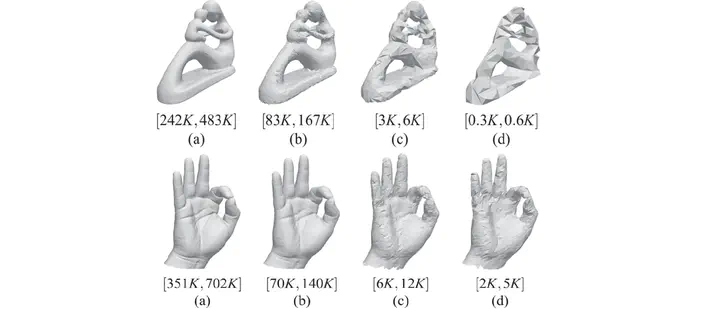
Simplicial complexes are widely used to discretize shapes. In low dimensions, a 3D shape is represented by discretizing its boundary surface, encoded as a triangle mesh, or by discretizing the enclosed volume, encoded as a tetrahedral mesh. High-dimensional simplicial complexes have recently found their application in topological data analysis. Topological data analysis aims at studying a point cloud P, possibly embedded in a high-dimensional metric space, by investigating the topological characteristics of the simplicial complexes built on P. Analysing such complexes is not feasible due to their size and dimensions. To this aim, the idea of simplifying a complex while preserving its topological features has been proposed in the literature. Here, we consider the problem of efficiently simplifying simplicial complexes in arbitrary dimensions. We provide a new definition for the edge contraction operator, based on a top-based data structure, with the objective of preserving structural aspects of a simplicial shape (i.e., its homology), and a new algorithm for verifying the link condition on a top-based representation. We implement the simplification algorithm obtained by coupling the new edge contraction and the link condition on a specific top-based data structure, that we use to demonstrate the scalability of our approach.