Efficient Computation and Simplification of Discrete Morse Decompositions on Triangulated Terrains
Abstract
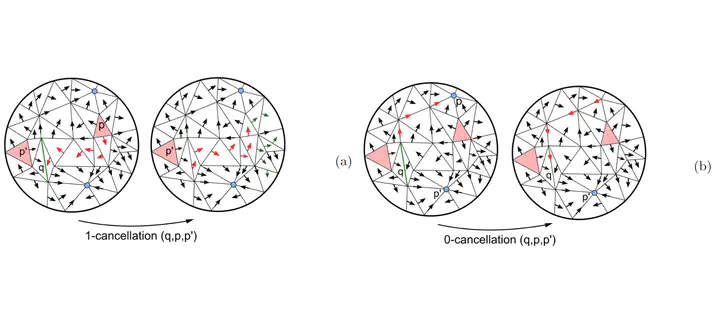
We consider the problem of efficient computing and simplifying Morse complexes on a Triangulated Irregular Network (TIN) based on discrete Morse theory. We develop a compact encoding for the discrete Morse gradient field, defined by the terrain elevation, by attaching it to the triangles of the TIN. This encoding is suitable to be combined with any TIN data structure storing just its vertices and triangles. We show how to compute such gradient field from the elevation values given at the TIN vertices, and how to simplify it effectively in order to reduce the number of critical elements. We demonstrate the effectiveness and scalability of our approach over large terrains by developing algorithms for extracting the cells of the Morse complexes as well as the graph joining the critical elements from the discrete gradient field. We compare implementations of our approach on a widely-used and compact adjacency-based topological data structure for a TIN and on a compact spatio-topological data structure that we have recently developed, the PR-star quadtree.