Abstract
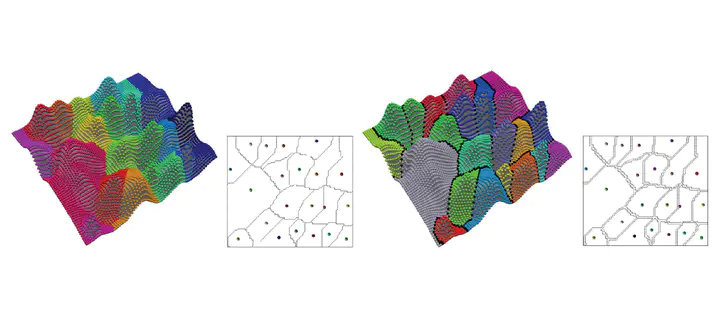
With improvements in sensor technology and simulation methods, datasets are growing in size, calling for the investigation of efficient and scalable tools for their analysis. Topological methods, able to extract essential features from data, are a prime candidate for the development of such tools. Here, we examine an approach based on discrete Morse theory and compare it to the well-known watershed approach as a means of obtaining Morse decompositions of tessellated manifolds endowed with scalar fields, such as triangulated terrains or tetrahedralized volume data. We examine the theoretical aspects as well as present empirical results based on synthetic and real-world data describing terrains and 3D scalar fields. We will show that the approach based on discrete Morse theory generates segmentations comparable to the watershed approach while being theoretically sound, more efficient with regard to time and space complexity, easily parallelizable, and allowing for the computation of all descending and ascending i-manifolds and the topological structure of the two Morse complexes.